详情
本书内容共计14章，分别从机器学习基础、简单线性回归、基于K临近法的分类和回归分析、特征提取和预处理、简单回归和多重回归、线性回归和逻辑回归、朴素贝叶斯、决策树的非线性分类和回归、决策树、随机森林和其他方法、感知机、向量机、人工神经网络、K-means聚类等内容。
书名：动手学深度学习
ISBN：978-7-115-49084-1
本书由人民邮电出版社发行数字版。版权所有，侵权必究。
您购买的人民邮电出版社电子书仅供您个人使用，未经授权，不得以任何方式复制和传播本书内容。
我们愿意相信读者具有这样的良知和觉悟，与我们共同保护知识产权。
如果购买者有侵权行为，我们可能对该用户实施包括但不限于关闭该帐号等维权措施，并可能追究法律责任。
著 阿斯顿·张（Aston Zhang）
李沐（Mu Li）
[美]扎卡里·C.立顿（Zachary C. Lipton）
[德]亚历山大· J.斯莫拉（Alexander J. Smola）
责任编辑 杨海玲
人民邮电出版社出版发行 北京市丰台区成寿寺路11号
邮编 100164 电子邮件 315@ptpress.com.cn
读者服务热线：(010)81055410
反盗版热线：(010)81055315
本书旨在为读者提供有关深度学习的交互式学习体验。书中不仅阐述深度学习的算法原理，还演示它们的实现和运行。与传统图书不同，本书的每一节都是一个可以下载并运行的 Jupyter记事本，它将文字、公式、图像、代码和运行结果结合在了一起。此外，读者还可以参与书中内容的讨论。
全书的内容分为3个部分：第一部分介绍深度学习的背景，提供预备知识，并包括深度学习最基础的概念和技术；第二部分描述深度学习计算的重要组成部分，还解释近年来令深度学习在多个领域大获成功的卷积神经网络和循环神经网络；第三部分评价优化算法，检验影响深度学习计算性能的重要因素，并分别列举深度学习在计算机视觉和自然语言处理中的重要应用。
本书同时覆盖深度学习的方法和实践，主要面向在校大学生、技术人员和研究人员。阅读本书需要读者了解基本的Python编程或附录中描述的线性代数、微分和概率基础。
这是一本及时且引人入胜的书。它不仅提供了深度学习原理的全面概述，还提供了具有编程代码的详细算法，此外，还提供了计算机视觉和自然语言处理中有关深度学习的最新介绍。如果你想钻研深度学习，请研读这本书！
韩家炜
ACM 院士、IEEE 院士
美国伊利诺伊大学香槟分校计算机系 Abel Bliss 教授
这是对机器学习文献的一个很受欢迎的补充，重点是通过集成Jupyter记事本实现的动手经验。深度学习的学生应该能体会到，这对于熟练掌握这一领域是非常宝贵的。
Bernhard Schölkopf
ACM 院士、德国国家科学院院士
德国马克斯•普朗克研究所智能系统院院长
这本书基于MXNet框架来介绍深度学习技术，书中代码可谓“所学即所用”，为喜欢通过Python代码进行学习的读者接触、了解深度学习技术提供了很大的便利。
周志华
ACM 院士、IEEE 院士、AAAS 院士
南京大学计算机科学与技术系主任
虽然业界已经有不错的深度学习方面的书籍，但都不够紧密结合工业界的应用实践。 我认为《动手学深度学习》是最适合工业界研发工程师学习的，因为这本书把算法理论、应用场景、代码实例都完美地联系在一起，引导读者把理论学习和应用实践紧密结合，知行合一，在动手中学习，在体会和领会中不断深化对深度学习的理解。 因此我毫无保留地向广大的读者强烈推荐《动手学深度学习》。
余凯
地平线公司创始人、首席执行官
强烈推荐这本书！它其实远不只是一本书：它不仅讲解深度学习背后的数学原理，更是一个编程工作台与记事本，让读者可以一边动手学习一边收到反馈，它还是个开源社区平台，让大家可以交流。作为在AI学术界和工业界都长期工作过的人，我特别赞赏这种手脑一体的学习方式，既能增强实践能力，又可以在解决问题中锻炼独立思考和批判性思维。
作者们是算法、工程兼强的业界翘楚，他们能奉献出这样的一本好的开源书，为他们点赞!
漆远
蚂蚁金服副总裁、首席人工智能科学家
这是一本基于Apache MXNet的深度学习实战书籍，可以帮助读者快速上手并掌握使用深度学习工具的基本技能。本书的几个作者都在机器学习领域有着非常丰富的经验。他们不光有大量的工业界实践经验，也有非常高的学术成就，所以对机器学习领域的前沿算法理解深刻。这使得作者们在提供优质代码的同时，也可以把最前沿的算法和概念深入浅出地介绍给读者。这本书可以帮助深度学习实践者快速提升自己的能力。
张潼
腾讯人工智能实验室主任
一年前作者开始在将门技术社群中做深度学习的系列讲座，当时我就对动手式讲座的内容和形式感到耳目一新。一年过去，看到《动手学深度学习》在持续精心打磨后终于成书出版，感觉十分欣喜！
深度学习是当前人工智能研究中的热门领域，吸引了大量感兴趣的开发者踊跃学习相关的开发技术。然而对大多数学习者而言，掌握深度学习是一件很不容易的事情，需要相继翻越数学基础、算法理论、编程开发、领域应用、软硬优化等几座大山。因此学习过程不容易一帆风顺，我也看到很多学习者还没进入开发环节就在理论学习的过程中抱憾放弃了。然而《动手学深度学习》却是一本很容易让学习者上瘾的书，它最大的特色是强调在动手编程中学习理论和培养实战能力。阅读本书最愉悦的感受是它很好地平衡了理论介绍和编程实操，内容简明扼要，衔接自然流畅，既反映了现代深度学习的进展，又兼具易学和实用特性，是深度学习爱好者难得的学习材料。特别值得称赞的是本书选择了Jupyter记事本作为开发学习环境，将教材、文档和代码统一起来，给读者提供了可以立即尝试修改代码和观察运行效果的交互式的学习体验，使学习充满了乐趣。
在过去的一年中，作者和社区成员对《动手学深度学习》进行了大量优化修改才得以成书，可以说这是一本深度学习前沿实践者给深度学习爱好者带来的诚心之作，相信大家都能在阅读和实践中拥有一样的共鸣。
沈强
将门创投创始合伙人
献给我们的家人
就在几年前，不管在大公司还是创业公司，都鲜有工程师和科学家将深度学习应用到智能产品与服务中。作为深度学习前身的神经网络，才刚刚摆脱被机器学习学术界认为是过时工具的印象。那个时候，即使是机器学习也非新闻头条的常客。它仅仅被看作是一门具有前瞻性，并拥有一系列小范围实际应用的学科。在包含计算机视觉和自然语言处理在内的实际应用通常需要大量的相关领域知识：这些实际应用被视为相互独立的领域，而机器学习只占其中一小部分。
然而仅仅在这几年之内，深度学习便令全世界大吃一惊。它非常有力地推动了计算机视觉、自然语言处理、自动语音识别、强化学习和统计建模等多个领域的快速发展。随着这些领域的不断进步，我们现在可以制造自动驾驶的汽车，基于短信、邮件甚至电话的自动回复系统，以及在围棋中击败最优秀人类选手的软件。这些由深度学习带来的新工具也正产生着广泛的影响：它们改变了电影制作和疾病诊断的方式，并在从天体物理学到生物学等各个基础科学中扮演越来越重要的角色。
与此同时，深度学习也给它的使用者们带来了独一无二的挑战：任何单一的应用都汇集了各学科的知识。具体来说，应用深度学习需要同时理解：
问题的动机和特点；
将大量不同类型神经网络层通过特定方式组合在一起的模型背后的数学原理；
在原始数据上拟合极复杂的深层模型的优化算法；
有效训练模型、避免数值计算陷阱以及充分利用硬件性能所需的工程技能；
为解决方案挑选合适的变量（超参数）组合的经验。
同样，我们几位作者也面临前所未有的挑战：我们需要在有限的篇幅里糅合深度学习的多方面知识，从而使读者能够较快理解并应用深度学习技术。本书代表了我们的一种尝试：我们将教给读者概念、背景知识和代码；我们将在同一个地方阐述剖析问题所需的批判性思维、解决问题所需的数学知识，以及实现解决方案所需的工程技能。
我们在2017年7月启动了写作这本书的项目。当时我们需要向用户解释Apache MXNet的新接口Gluon。遗憾的是，我们并没有找到任何一个资源可以同时满足以下几点需求：
包含较新的方法和应用，并不断更新；
广泛覆盖现代深度学习技术并具有一定的技术深度；
既是严谨的教科书，又是包含可运行代码的生动的教程。
那时，我们在博客和GitHub上找到了大量的演示特定深度学习框架（例如用TensorFlow进行数值计算）或实现特定模型（例如AlexNet、ResNet等）的示例代码。这些示例代码的一大价值在于提供了教科书或论文往往省略的实现细节，比如数据的处理和运算的高效率实现。如果不了解这些，即使能将算法倒背如流，也难以将算法应用到自己的项目中去。此外，这些示例代码还使得用户能通过观察修改代码所导致的结果变化而快速验证想法、积累经验。因此，我们坚信动手实践对于学习深度学习的重要性。然而可惜的是，这些示例代码通常侧重于如何实现给定的方法，却忽略了有关算法设计的探究或者实现细节的解释。虽然在像Distill这样的网站和某些博客上出现了一些有关算法设计和实现细节的讨论，但它们常常缺少示例代码，并通常仅覆盖深度学习的一小部分。
另外，我们欣喜地看到了一些有关深度学习的教科书不断问世，其中最著名的要数Goodfellow、Bengio和Courville的《深度学习》。该书梳理了深度学习背后的众多概念与方法，是一本极为优秀的教材。然而，这类资源并没有将概念描述与实际代码相结合，以至于有时会令读者对如何实现它们感到毫无头绪。除了这些以外，商业课程提供者们虽然制作了众多的优质资源，但它们的付费门槛令不少用户望而生畏。
正因为这样，深度学习用户，尤其是初学者，往往不得不参考来源不同的多种资料。例如，通过教科书或者论文来掌握算法及相关数学知识，阅读线上文档学习深度学习框架的使用方法，然后寻找感兴趣的算法在这个框架上的实现，并摸索如何将它应用到自己的项目中去。如果你正亲身经历这一过程，你可能会感到痛苦：不同来源的资料有时难以相互一一对应，即便能够对应也可能需要花费大量的精力。例如，我们需要将某篇论文公式中的数学变量与某段网上实现中的程序变量一一对应，并在代码中找到论文可能没交代清楚的实现细节，甚至要为运行不同的代码安装不同的运行环境。
针对以上存在的痛点，我们正在着手创建一个为实现以下目标的统一资源：
所有人均可在网上免费获取；
提供足够的技术深度，从而帮助读者实际成为深度学习应用科学家——既理解数学原理，又能够实现并不断改进方法；
包含可运行的代码，为读者展示如何在实际中解决问题，这样不仅直接将数学公式对应成实际代码，而且可以修改代码、观察结果并及时获取经验；
允许我们和整个社区不断快速迭代内容，从而紧跟仍在高速发展的深度学习领域；
由包含有关技术细节问答的论坛作为补充，使大家可以相互答疑并交换经验。
这些目标往往互有冲突：公式、定理和引用最容易通过LaTeX进行管理和展示，代码自然应该用简单易懂的Python描述，而网页本身应该是一堆HTML及配套的CSS和JavaScript。此外，我们希望这个资源可以作为可执行代码、实体书以及网站。然而，目前并没有任何工具可以完美地满足以上所有需求。
因此，我们不得不自己来集成这样的一个工作流。我们决定在GitHub上分享源代码并允许提交编辑，通过Jupyter记事本来整合代码、公式、文本、图片等，使用Sphinx作为渲染引擎来生成不同格式的输出，并使用Discourse作为论坛。虽然我们的系统尚未完善，但这些选择在互有冲突的目标之间取得了较好的折中。这很可能是使用这种集成工作流发布的第一本书。
本书的两位中国作者曾每周末在线免费讲授“动手学深度学习”系列课程。课程的讲义自然成为了本书内容的蓝本。这个课程持续了5个月，其间近3 000名同学参与了讨论，并贡献了5 000多个有价值的讨论，特别是其中几个参加比赛的练习很受欢迎。这个课程的受欢迎程度出乎我们的意料。尽管我们将课件和课程视频都公开在了网上，但我们同时觉得出版成纸质书也许能让更多喜爱阅读的读者受益。因此，我们委托人民邮电出版社来出版这本书。
从蓝本到成书花费了更多的时间。我们对涉及的所有技术点补充了背景介绍，并使用了更加严谨的写作风格，还对版式和示意图做了大量修改。书中所有的代码执行结果都是自动生成的，任何改动都会触发对书中每一段代码的测试，以保证读者在动手实践时能复现结果。
我们的初衷是让更多人更容易地使用深度学习。为了让大家能够便利地获取这些资源，我们保留了免费的网站内容，并且通过不收取稿费的方式来降低纸质书的价格，使更多人有能力购买。
我们无比感谢本书的中英文版稿件贡献者和论坛用户。他们帮助增添或改进了书中内容并提供了有价值的反馈。特别地，我们要感谢每一位为这本中文版开源书提交内容改动的贡献者。这些贡献者的GitHub用户名或姓名是（排名不分先后）：许致中、邓杨、崔永明、Aaron Sun、陈斌斌、曾元豪、周长安、李昂、王晨光、Chaitanya Prakash Bapat、金杰、赵小华、戴作卓、刘捷、张建浩、梓善、唐佐林、DHRUV536、丁海、郭晶博、段弘、杨英明、林海滨、范舟、李律、李阳、夏鲁豫、张鹏、徐曦、Kangel Zenn、Richard CUI、郭云鹏、hank123456、金颢、hardfish82、何通、高剑伟、王海龙、htoooth、hufuyu、Kun Hu、刘俊朋、沈海晨、韩承宇、张钟越、罗晶、jiqirer、贾忠祥、姜蔚蔚、田宇琛、王曜、李凯、兰青、王乐园、Leonard Lausen、张雷、鄭宇翔、linbojin、lingss0918、杨大卫、刘佳、戴玮、贾老坏、陆明、张亚鹏、李超、周俊佐、Liang Jinzheng、童话、彭小平、王皓、彭大发、彭远卓、黄瓒、解浚源、彭艺宇、刘铭、吴俊、刘睿、张绍明、施洪、刘天池、廖翊康、施行健、孙畔勇、查晟、郑帅、任杰骥、王海珍、王鑫、wangzhe258369、王振荟、周军、吴侃、汪磊、wudayo、徐驰、夏根源、何孝霆、谢国超、刘新伟、肖梅峰、黄晓烽、燕文磊、王贻达、马逸飞、邱怡轩、吴勇、杨培文、余峰、Peng Yu、王雨薇、王宇翔、喻心悦、赵越、刘忆智、张航、郑达、陈志、周航、张帜、周远、汪汇泽、谢乘胜、aitehappiness、张满闯、孙焱、林健、董进、陈宇泓、魏耀武、田慧嫒、陈琛、许柏楠、bowcr、张宇楠、王晨、李居正、王宗冰、刘垣德。谢谢你们帮忙改进这本书。
本书的初稿在中国科学技术大学、上海财经大学的“深度学习”课程，以及浙江大学的“物联网与信息处理”课程和上海交通大学的“面向视觉识别的卷积神经网络”课程中被用于教学。我们在此感谢这些课程的师生，特别是连德富教授、王智教授和罗家佳教授，感谢他们对改进本书提供的宝贵意见。
此外，我们感谢Amazon Web Services，特别是Swami Sivasubramanian、Raju Gulabani、Charlie Bell和Andrew Jassy在我们撰写本书时给予的慷慨支持。如果没有可用的时间、资源以及来自同事们的讨论和鼓励，就没有这本书的项目。我们还要感谢Apache MXNet团队实现了很多本书所使用的特性。另外，经过同事们的校勘，本书的质量得到了极大的提升。在此我们一一列出章节和校勘人，以表示我们由衷的感谢：引言的校勘人为金颢，预备知识的校勘人为吴俊，深度学习基础的校勘人为张航、王晨光、林海滨，深度学习计算的校勘人为查晟，卷积神经网络的校勘人为张帜、何通，循环神经网络的校勘人为查晟，优化算法的校勘人为郑帅，计算性能的校勘人为郑达、吴俊，计算机视觉的校勘人为解浚源、张帜、何通、张航，自然语言处理的校勘人为王晨光，附录的校勘人为金颢。
感谢将门创投，特别是王慧、高欣欣、常铭珊和白玉，为本书的两位中国作者讲授“动手学深度学习”系列课程提供了平台。感谢所有参与这一系列课程的数千名同学们。感谢Amazon Web Services中国团队的同事们，特别是费良宏和王晨对作者的支持与鼓励。感谢本书论坛的3位版主：王鑫、夏鲁豫和杨培文。他们牺牲了自己宝贵的休息时间来回复大家的提问。感谢人民邮电出版社的杨海玲编辑为我们在本书的出版过程中提供的各种帮助。
最后，我们要感谢我们的家人。谢谢你们一直陪伴着我们。
本书的英文版Dive into Deep Learning是加州大学伯克利分校2019年春学期“Introduction to Deep Learning”（深度学习导论）课程的教材。截至2019年春学期，本书中的内容已被全球15所知名大学用于教学。本书的学习社区、免费教学资源（课件、教学视频、更多习题等），以及用于本书学习或教学的免费计算资源（仅限学生和老师）的申请方法在本书网站 https://zh.d2l.ai 上发布。诚然，将算法、公式、图片、代码和样例统一进一本适合阅读的书，并以具有交互式体验的Jupyter记事本文件的形式提供给读者，是对我们的极大挑战。书中难免有很多疏忽的地方，敬请原谅，并希望读者能通过每一节后面的二维码向我们反馈阅读本书过程中发现的问题。
结尾处，附上陆游的一句诗作为勉励：
“纸上得来终觉浅，绝知此事要躬行。”
阿斯顿·张、李沐、扎卡里· C. 立顿、亚历山大· J. 斯莫拉
2019年5月
本书将全面介绍深度学习从模型构造到模型训练的方方面面，以及它们在计算机视觉和自然语言处理中的应用。我们不仅将阐述算法原理，还将基于Apache MXNet对算法进行实现，并实际运行它们。本书的每一节都是一个Jupyter记事本。它将文字、公式、图像、代码和运行结果结合在了一起。读者不但能直接阅读它们，而且可以运行它们以获得交互式的学习体验。
本书面向希望了解深度学习，特别是对实际使用深度学习感兴趣的大学生、工程师和研究人员。本书并不要求读者有任何深度学习或者机器学习的背景知识，我们将从头开始解释每一个概念。虽然深度学习技术与应用的阐述涉及了数学和编程，但读者只需了解基础的数学和编程，如基础的线性代数、微分和概率，以及基本的Python编程知识。在附录A中我们提供了本书涉及的主要数学知识供读者参考。如果读者之前没有接触过Python，可以参考其中文教程或英文教程。当然，如果读者只对本书中的数学部分感兴趣，可以忽略掉编程部分，反之亦然。
本书内容大体可以分为3个部分。
第一部分（第1章~第3章）涵盖预备工作和基础知识。第1章介绍深度学习的背景。第2章提供动手学深度学习所需要的预备知识，例如，如何获取并运行本书中的代码。第3章包括深度学习最基础的概念和技术，如多层感知机和模型正则化。如果读者时间有限，并且只想了解深度学习最基础的概念和技术，那么只需阅读第一部分。
第二部分（第4章~第6章）关注现代深度学习技术。第4章描述深度学习计算的各个重要组成部分，并为实现后续更复杂的模型打下基础。第5章解释近年来令深度学习在计算机视觉领域大获成功的卷积神经网络。第6章阐述近年来常用于处理序列数据的循环神经网络。阅读第二部分有助于掌握现代深度学习技术。
第三部分（第7章~第10章）讨论计算性能和应用。第7章评价各种用来训练深度学习模型的优化算法。第8章检验影响深度学习计算性能的几个重要因素。第9章和第10章分别列举深度学习在计算机视觉和自然语言处理中的重要应用。这部分内容读者可根据兴趣选择阅读。
图0-1描绘了本书的结构，其中由A章指向B章的箭头表明A章的知识有助于理解B章的内容。
图0-1 本书的结构
本书的一大特点是每一节的代码都是可以运行的。读者可以改动代码后重新运行，并通过运行结果进一步理解改动所带来的影响。我们认为，这种交互式的学习体验对于学习深度学习非常重要。因为深度学习目前并没有很好的理论解释框架，很多论断只可意会。文字解释在这时候可能比较苍白无力，而且不足以覆盖所有细节。读者需要不断改动代码、观察运行结果并总结经验，从而逐步领悟和掌握深度学习。
本书的代码基于Apache MXNet实现。MXNet是一个开源的深度学习框架。它是AWS（亚马逊云计算服务）首选的深度学习框架，也被众多学校和公司使用。为了避免重复描述，我们将本书中多次使用的函数和类封装在d2lzh包中（包的名称源于本书的网站地址）。这些函数和类的定义的所在章节已在附录F里列出。但是，因为深度学习发展极为迅速，未来版本的MXNet可能会造成书中部分代码无法正常运行。遇到相关问题可参考2.1节来更新代码和运行环境。如果读者想了解运行本书代码所依赖的MXNet和d2lzh包的版本号，也可参考2.1节。
我们提供代码的主要目的在于增加一个在文字、图像和公式外的学习深度学习算法的方式，以及一个便于理解各个算法在真实数据上的实际效果的交互式环境。书中只使用了MXNet的ndarray、autograd、gluon等模块或包的基础功能，从而使读者尽可能了解深度学习算法的实现细节。即便读者在研究和工作中使用的是其他深度学习框架，书中的代码也有助于读者更好地理解和应用深度学习算法。
本书的网站是https://zh.d2l.ai，上面提供了学习社区地址和GitHub开源地址。如果读者对书中某节内容有疑惑，可扫一扫该节开始的二维码参与该节内容的讨论。值得一提的是，在有关Kaggle比赛章节的讨论区中，众多社区成员提供了丰富的高水平方法，我们强烈推荐给大家。希望诸位积极参与学习社区中的讨论，并相信大家一定会有所收获。本书作者和MXNet开发人员也时常参与社区中的讨论。
本书由异步社区出品，社区（https://www.epubit.com/）为您提供相关资源和后续服务。
本书提供如下资源：
本书源代码；
书中彩图文件。
要获得以上配套资源，请在异步社区本书页面中点击
，跳转到下载界面，按提示进行操作即可。注意：为保证购书读者的权益，该操作会给出相关提示，要求输入提取码进行验证。
如果您是教师，希望获得教学配套资源，请在社区本书页面中直接联系本书的责任编辑。
作者和编辑尽最大努力来确保书中内容的准确性，但难免会存在疏漏。欢迎您将发现的问题反馈给我们，帮助我们提升图书的质量。
当您发现错误时，请登录异步社区，按书名搜索，进入本书页面，点击“提交勘误”，输入勘误信息，点击“提交”按钮即可。本书的作者和编辑会对您提交的勘误进行审核，确认并接受后，您将获赠异步社区的100积分。积分可用于在异步社区兑换优惠券、样书或奖品。
我们的联系邮箱是contact@epubit.com.cn。
如果您对本书有任何疑问或建议，请您发邮件给我们，并请在邮件标题中注明本书书名，以便我们更高效地做出反馈。
如果您有兴趣出版图书、录制教学视频，或者参与图书翻译、技术审校等工作，可以发邮件给我们；有意出版图书的作者也可以到异步社区在线提交投稿（直接访问www.epubit.com/selfpublish/submission即可）。
如果您是学校、培训机构或企业，想批量购买本书或异步社区出版的其他图书，也可以发邮件给我们。
如果您在网上发现有针对异步社区出品图书的各种形式的盗版行为，包括对图书全部或部分内容的非授权传播，请您将怀疑有侵权行为的链接发邮件给我们。您的这一举动是对作者权益的保护，也是我们持续为您提供有价值的内容的动力之源。
“异步社区”是人民邮电出版社旗下IT专业图书社区，致力于出版精品IT技术图书和相关学习产品，为作译者提供优质出版服务。异步社区创办于2015年8月，提供大量精品IT技术图书和电子书，以及高品质技术文章和视频课程。更多详情请访问异步社区官网https://www.epubit.com。
“异步图书”是由异步社区编辑团队策划出版的精品IT专业图书的品牌，依托于人民邮电出版社近30年的计算机图书出版积累和专业编辑团队，相关图书在封面上印有异步图书的LOGO。异步图书的出版领域包括软件开发、大数据、AI、测试、前端、网络技术等。
异步社区
微信服务号
数相关符号
| 符 号 |
含 义 |
|---|---|
| x |
标量 |
| x |
向量 |
| X |
矩阵 |
|
|
张量 |
集合相关符号
| 符 号 |
含 义 |
|---|---|
| χ |
集合 |
|
|
实数集合 |
|
|
n维的实数向量集合 |
|
|
x行y列的实数矩阵集合 |
操作符相关符号
| 符 号 |
含 义 |
|---|---|
| (⋅)⊤ |
向量或矩阵的转置 |
|
|
按元素相乘，即阿达马（Hadamard）积 |
| |χ| |
集合χ中元素个数 |
|
|
Lp范数 |
|
|
L2范数 |
|
|
连加 |
|
|
连乘 |
函数相关符号
| 符 号 |
含 义 |
|---|---|
| f (·) |
函数 |
| log(·) |
自然对数函数 |
| exp(·) |
指数函数 |
导数和梯度相关符号
| 符 号 |
含 义 |
|---|---|
|
|
y关于x的导数 |
|
|
y关于x的偏导数 |
|
|
y关于·的梯度 |
概率和统计相关符号
| 符 号 |
含 义 |
|---|---|
| P(·) |
概率分布 |
| ·~ P |
随机变量·的概率分布是P |
| P(·|·) |
条件概率分布 |
| E.( f (·)) |
函数f (·)对·的数学期望 |
复杂度相关符号
| 符 号 |
含 义 |
|---|---|
|
|
大O符号（渐进符号） |
从本章开始，我们将探索深度学习的奥秘。作为机器学习的一类，深度学习通常基于神经网络模型逐级表示越来越抽象的概念或模式。我们先从线性回归和softmax回归这两种单层神经网络入手，简要介绍机器学习中的基本概念。然后，我们由单层神经网络延伸到多层神经网络，并通过多层感知机引入深度学习模型。在观察和了解了模型的过拟合现象后，我们将介绍深度学习中应对过拟合的常用方法——权重衰减和丢弃法。接着，为了进一步理解深度学习模型训练的本质，我们将详细解释正向传播和反向传播。掌握这两个概念后，我们能更好地认识深度学习中的数值稳定性和初始化的一些问题。最后，我们通过一个深度学习应用案例对本章内容学以致用。
在本章的前几节，我们先介绍单层神经网络——线性回归和softmax回归。
扫码直达讨论区
线性回归输出是一个连续值，因此适用于回归问题。回归问题在实际中很常见，如预测房屋价格、气温、销售额等连续值的问题。与回归问题不同，分类问题中模型的最终输出是一个离散值。我们所说的图像分类、垃圾邮件识别、疾病检测等输出为离散值的问题都属于分类问题的范畴。softmax回归则适用于分类问题。
由于线性回归和softmax 回归都是单层神经网络，它们涉及的概念和技术同样适用于大多数的深度学习模型。我们首先以线性回归为例，介绍大多数深度学习模型的基本要素和表示方法。
我们以一个简单的房屋价格预测作为例子来解释线性回归的基本要素。这个应用的目标是预测一栋房子的售出价格（元）。我们知道这个价格取决于很多因素，如房屋状况、地段、市场行情等。为了简单起见，这里我们假设价格只取决于房屋状况的两个因素，即面积（平方米）和房龄（年）。接下来我们希望探索价格与这两个因素的具体关系。
设房屋的面积为x1，房龄为x2，售出价格为y。我们需要建立基于输入x1 和x2来计算输出y的表达式，也就是模型（model）。顾名思义，线性回归假设输出与各个输入之间是线性关系：
其中
和
是权重（weight），b是偏差（bias），且均为标量。它们是线性回归模型的参数（parameter）。模型输出
是线性回归对真实价格 y的预测或估计。我们通常允许它们之间有一定误差。
接下来我们需要通过数据来寻找特定的模型参数值，使模型在数据上的误差尽可能小。这个过程叫作模型训练（model training）。下面我们介绍模型训练所涉及的3个要素。
我们通常收集一系列的真实数据，例如多栋房屋的真实售出价格和它们对应的面积和房龄。我们希望在这个数据上面寻找模型参数来使模型的预测价格与真实价格的误差最小。在机器学习术语里，该数据集被称为训练数据集（training data set）或训练集（training set），一栋房屋被称为一个样本（sample），其真实售出价格叫作标签（label），用来预测标签的两个因素叫作特征（feature）。特征用来表征样本的特点。
假设我们采集的样本数为n，索引为i的样本的特征为
和
，标签为
。对于索引为i的房屋，线性回归模型的房屋价格预测表达式为
在模型训练中，我们需要衡量价格预测值与真实值之间的误差。通常我们会选取一个非负数作为误差，且数值越小表示误差越小。一个常用的选择是平方函数。它在评估索引为i 的样本误差的表达式为
其中常数1/2使对平方项求导后的常数系数为 1，这样在形式上稍微简单一些。显然，误差越小表示预测价格与真实价格越相近，且当二者相等时误差为 0。给定训练数据集，这个误差只与模型参数相关，因此我们将它记为以模型参数为参数的函数。在机器学习里，将衡量误差的函数称为损失函数（loss function）。这里使用的平方误差函数也称为平方损失（square loss）。
通常，我们用训练数据集中所有样本误差的平均来衡量模型预测的质量，即
在模型训练中，我们希望找出一组模型参数，记为
，来使训练样本平均损失最小：
当模型和损失函数形式较为简单时，上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解（analytical solution）。本节使用的线性回归和平方误差刚好属于这个范畴。然而，大多数深度学习模型并没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解（numerical solution）。
在求数值解的优化算法中，小批量随机梯度下降（mini-batch stochastic gradient descent）在深度学习中被广泛使用。它的算法很简单：先选取一组模型参数的初始值，如随机选取；接下来对参数进行多次迭代，使每次迭代都可能降低损失函数的值。在每次迭代中，先随机均匀采样一个由固定数目训练数据样本所组成的小批量（mini-batch）
，然后求小批量中数据样本的平均损失有关模型参数的导数（梯度），最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。
在训练本节讨论的线性回归模型的过程中，模型的每个参数将作如下迭代：
在上式中，
代表每个小批量中的样本个数（批量大小，batch size），η称作学习率（learning rate）并取正数。需要强调的是，这里的批量大小和学习率的值是人为设定的，并不是通过模型训练学出的，因此叫作超参数（hyperparameter）。我们通常所说的“调参”指的正是调节超参数，例如通过反复试错来找到超参数合适的值。在少数情况下，超参数也可以通过模型训练学出。本书对此类情况不做讨论。
模型训练完成后，我们将模型参数
在优化算法停止时的值分别记作
。注意，这里我们得到的并不一定是最小化损失函数的最优解，而是对最优解的一个近似。然后，我们就可以使用学出的线性回归模型
来估算训练数据集以外任意一栋面积（平方米）为
、房龄（年）为
的房屋的价格了。这里的估算也叫作模型预测、模型推断或模型测试。
我们已经阐述了线性回归的模型表达式、训练和预测。下面我们解释线性回归与神经网络的联系，以及线性回归的矢量计算表达式。
在深度学习中，我们可以使用神经网络图直观地表现模型结构。为了更清晰地展示线性回归作为神经网络的结构，图3-1 使用神经网络图表示本节中介绍的线性回归模型。神经网络图隐去了模型参数权重和偏差。
图3-1 线性回归是一个单层神经网络
在图3-1所示的神经网络中，输入分别为x1 和x2，因此输入层的输入个数为 2。输入个数也叫特征数或特征向量维度。图3-1中网络的输出为o，输出层的输出个数为 1。需要注意的是，我们直接将图3-1 中神经网络的输出o作为线性回归的输出，即
。由于输入层并不涉及计算，按照惯例，图3-1 所示的神经网络的层数为 1。所以，线性回归是一个单层神经网络。输出层中负责计算o的单元又叫神经元。在线性回归中，o的计算依赖于x1和x2。也就是说，输出层中的神经元和输入层中各个输入完全连接。因此，这里的输出层又叫全连接层（fully-connected layer）或稠密层 ( dense layer）。
在模型训练或预测时，我们常常会同时处理多个数据样本并用到矢量计算。在介绍线性回归的矢量计算表达式之前，让我们先考虑对两个向量相加的两种方法。
下面先定义两个 1 000 维的向量。
In [1]: from mxnet import nd
from time import time
a = nd.ones(shape=1000)
b = nd.ones(shape=1000)向量相加的一种方法是，将这两个向量按元素逐一做标量加法。
In [2]: start = time()
c = nd.zeros(shape=1000)
for i in range(1000):
c[i] = a[i] + b[i]
time() - start
Out[2]: 0.16967248916625977向量相加的另一种方法是，将这两个向量直接做矢量加法。
In [3]: start = time()
d = a + b
time() - start
Out[3]: 0.00031185150146484375结果很明显，后者比前者更省时。因此，我们应该尽可能采用矢量计算，以提升计算效率。
让我们再次回到本节的房价预测问题。如果我们对训练数据集里的3个房屋样本（索引分别为1、2和3）逐一预测价格，将得到
现在，我们将上面3个等式转化成矢量计算。设
对 3 个房屋样本预测价格的矢量计算表达式为
，其中的加法运算使用了广播机制（参见2.2节）。例如：
In [4]: a = nd.ones(shape=3)
b = 10
a + b
Out[4]:
[11. 11. 11.]
<NDArray 3 @cpu(0)>广义上讲，当数据样本数为n，特征数为d时，线性回归的矢量计算表达式为
其中模型输出
，批量数据样本特征
，权重
， 偏差
。相应地，批量数据样本标签
。设模型参数
，我们可以重写损失函数为
小批量随机梯度下降的迭代步骤将相应地改写为
其中梯度是损失有关3个为标量的模型参数的偏导数组成的向量：
小结
- 和大多数深度学习模型一样，对于线性回归这样一种单层神经网络，它的基本要素包括模型、训练数据、损失函数和优化算法。
- 既可以用神经网络图表示线性回归，又可以用矢量计算表示该模型。
- 应该尽可能采用矢量计算，以提升计算效率。
练习
使用其他包（如 NumPy）或其他编程语言（如 MATLAB），比较相加两个向量的两种方法的运行时间。
扫码直达讨论区
在了解了线性回归的背景知识之后，现在我们可以动手实现它了。尽管强大的深度学习框架可以减少大量重复性工作，但若过于依赖它提供的便利，会导致我们很难深入理解深度学习是如何工作的。因此，本节将介绍如何只利用NDArray和autograd来实现一个线性回归的训练。
首先，导入本节中实验所需的包或模块，其中的matplotlib包可用于作图，且设置成嵌入显示。
In [1]: %matplotlib inline
from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd, nd
import random我们构造一个简单的人工训练数据集，它可以使我们能够直观比较学到的参数和真实的模型参数的区别。设训练数据集样本数为 1000，输入个数（特征数）为2。给定随机生成的批量样本特征
，我们使用线性回归模型真实权重
和偏差
，以及一个随机噪声项ϵ来生成标签
其中噪声项ϵ服从均值为 0、标准差为 0.01 的正态分布。噪声代表了数据集中无意义的干扰。下面，让我们生成数据集。
In [2]: num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)注意，features的每一行是一个长度为 2 的向量，而labels的每一行是一个长度为1的向量（标量）。
In [3]: features[0], labels[0]
Out[3]: (
[2.2122064 0.7740038]
<NDArray 2 @cpu(0)>,
[6.000587]
<NDArray 1 @cpu(0)>)通过生成第二个特征features[:, 1]和标签labels的散点图，可以更直观地观察两者间的线性关系。
In [4]: def use_svg_display():
# 用矢量图显示
display.set_matplotlib_formats('svg')
def set_f igsize(f igsize=(3.5, 2.5)):
use_svg_display()
# 设置图的尺寸
plt.rcParams['f igure.f igsize'] = f igsize
set_f igsize()
plt.scatter(features[:, 1].asnumpy(), labels.asnumpy(), 1); # 加分号只显示图我们将上面的plt作图函数以及use_svg_display函数和set_f igsize函数定义在d2lzh包里。以后在作图时，我们将直接调用d2lzh.plt。由于plt在d2lzh包中是一个全局变量，我们在作图前只需要调用d2lzh.set_figsize()即可打印矢量图并设置图的尺寸。
在训练模型的时候，我们需要遍历数据集并不断读取小批量数据样本。这里我们定义一个函数：它每次返回batch_size（批量大小）个随机样本的特征和标签。
In [5]: # 本函数已保存在d2lzh包中方便以后使用
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuff le(indices) # 样本的读取顺序是随机的
for i in range(0, num_examples, batch_size):
j = nd.array(indices[i: min(i + batch_size, num_examples)])
yield features.take(j), labels.take(j) # take函数根据索引返回对应元素让我们读取第一个小批量数据样本并打印。每个批量的特征形状为(10, 2)，分别对应批量大小和输入个数；标签形状为批量大小。
In [6]: batch_size = 10
for X, y in data_iter(batch_size, features, labels):
print(X, y)
break
[[ 1.0876857 -1.7063738 ]
[-0.51129895 0.46543437]
[ 0.1533563 -0.735794 ]
[ 0.3717077 0.9300072 ]
[ 1.0115732 -0.83923554]
[ 1.9738784 0.81172043]
[-1.771029 -0.45138445]
[ 0.7465509 -0.5054337 ]
[-0.52480155 0.3005414 ]
[ 0.5583534 -0.6039059 ]]
<NDArray 10x2 @cpu(0)>
[12.174357 1.6139998 6.9870367 1.7626053 9.06552 5.3893285
2.1933131 7.4012175 2.1383817 7.379732 ]
<NDArray 10 @cpu(0)>我们将权重初始化成均值为 0、标准差为 0.01 的正态随机数，偏差则初始化成 0。
In [7]: w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))
b = nd.zeros(shape=(1,))之后的模型训练中，需要对这些参数求梯度来迭代参数的值，因此我们需要创建它们的梯度。
In [8]: w.attach_grad()
b.attach_grad()下面是线性回归的矢量计算表达式的实现。我们使用dot函数做矩阵乘法。
In [9]: def linreg(X, w, b): # 本函数已保存在d2lzh包中方便以后使用
return nd.dot(X, w) + b我们使用3.1节描述的平方损失来定义线性回归的损失函数。在实现中，我们需要把真实值y变形成预测值y_hat的形状。以下函数返回的结果也将和y_hat的形状相同。
In [10]: def squared_loss(y_hat, y): # 本函数已保存在d2lzh包中方便以后使用
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2以下的sgd函数实现了3.1节中介绍的小批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数。这里自动求梯度模块计算得来的梯度是一个批量样本的梯度和。我们将它除以批量大小来得到平均值。
In [11]: def sgd(params, lr, batch_size): # 本函数已保存在d2lzh包中方便以后使用
for param in params:
param[:] = param - lr * param.grad / batch_size在训练中，我们将多次迭代模型参数。在每次迭代中，我们根据当前读取的小批量数据样本（特征X和标签y），通过调用反向函数backward计算小批量随机梯度，并调用优化算法sgd迭代模型参数。由于我们之前设批量大小batch_size为 10，每个小批量的损失l的形状为(10, 1)。回忆一下2.3节。由于变量l并不是一个标量，运行l.backward()将对l中元素求和得到新的变量，再求该变量有关模型参数的梯度。
在一个迭代周期（epoch）中，我们将完整遍历一遍data_iter函数，并对训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设3和 0.03。在实践中，大多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得越大模型可能越有效，但是训练时间可能过长。我们会在后面第7章中详细介绍学习率对模型的影响。
In [12]: lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs): # 训练模型一共需要num_epochs个迭代周期
# 在每一个迭代周期中, 会使用训练数据集中所有样本一次（假设样本数能够被批量大小整除）。X
# 和y分别是小批量样本的特征和标签
for X, y in data_iter(batch_size, features, labels):
with autograd.record():
l = loss(net(X, w, b), y) # l是有关小批量X和y的损失
l.backward() # 小批量的损失对模型参数求梯度
sgd([w, b], lr, batch_size) # 使用小批量随机梯度下降迭代模型参数
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))
epoch 1, loss 0.040436
epoch 2, loss 0.000155
epoch 3, loss 0.000050 训练完成后，我们可以比较学到的参数和用来生成训练集的真实参数。它们应该很接近。
In [13]: true_w, w
Out[13]: ([2, -3.4],
[[ 1.9996936]
[-3.3997262]]
<NDArray 2x1 @cpu(0)>)
In [14]: true_b, b
Out[14]: (4.2,
[4.199704]
<NDArray 1 @cpu(0)>)小结
- 可以看出，仅使用
NDArray和autograd模块就可以很容易地实现一个模型。接下来，本书会在此基础上描述更多深度学习模型，并介绍怎样使用更简洁的代码（见3.3节）来实现它们。练习
（1）为什么
squared_loss函数中需要使用reshape函数?（2）尝试使用不同的学习率，观察损失函数值的下降快慢。
（3）如果样本个数不能被批量大小整除，
data_iter函数的行为会有什么变化？
扫码直达讨论区
随着深度学习框架的发展，开发深度学习应用变得越来越便利。实践中，我们通常可以用比3.2节更简洁的代码来实现同样的模型。在本节中，我们将介绍如何使用 MXNet 提供的Gluon接口更方便地实现线性回归的训练。
我们生成与3.2节中相同的数据集。其中features是训练数据特征，labels是标签。
In [1]: from mxnet import autograd, nd
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)Gluon 提供了data包来读取数据。由于data常用作变量名，我们将导入的data模块用添加了 Gluon 首字母的假名gdata代替。在每一次迭代中，我们将随机读取包含 10 个数据样本的小批量。
In [2]: from mxnet.gluon import data as gdata
batch_size = 10
# 将训练数据的特征和标签组合
dataset = gdata.ArrayDataset(features, labels)
# 随机读取小批量
data_iter = gdata.DataLoader(dataset, batch_size, shuff le=True) 这里data_iter的使用与3.2节中的一样。让我们读取并打印第一个小批量数据样本。
In [3]: for X, y in data_iter:
print(X, y)
break
[[-1.4011667 -1.108803 ]
[-0.4813231 0.5334126 ]
[ 0.57794803 0.72061497]
[ 1.1208912 1.2570045 ]
[-0.2504259 -0.45037505]
[ 0.08554042 0.5336134 ]
[ 0.6347856 1.5795654 ]
[-2.118665 3.3493772 ]
[ 1.1353118 0.99125063]
[-0.4814555 -0.91107726]]
<NDArray 10x2 @cpu(0)>
[ 5.16208 1.4169512 2.9065104 2.164263 5.215756
2.558468 0.09139667 -11.421704 3.1042643 6.332793 ]
<NDArray 10 @cpu(0)>在3.2节从零开始的实现中，我们需要定义模型参数，并使用它们一步步描述模型是怎样计算的。当模型结构变得更复杂时，这些步骤将变得更烦琐。其实，Gluon 提供了大量预定义的层，这使我们只需关注使用哪些层来构造模型。下面将介绍如何使用 Gluon 更简洁地定义线性回归。
首先，导入nn模块。实际上，“nn”是 neural networks（神经网络）的缩写。顾名思义，该模块定义了大量神经网络的层。我们先定义一个模型变量net，它是一个 Sequential实例。在 Gluon 中，Sequential实例可以看作是一个串联各个层的容器。在构造模型时，我们在该容器中依次添加层。当给定输入数据时，容器中的每一层将依次计算并将输出作为下一层的输入。
In [4]: from mxnet.gluon import nn
net = nn.Sequential()回顾图3-1 中线性回归在神经网络图中的表示。作为一个单层神经网络，线性回归输出层中的神经元和输入层中各个输入完全连接。因此，线性回归的输出层又叫全连接层。在 Gluon 中，全连接层是一个Dense实例。我们定义该层输出个数为 1。
In [5]: net.add(nn.Dense(1))值得一提的是，在 Gluon 中我们无须指定每一层输入的形状，例如线性回归的输入个数。当模型得到数据时，例如后面执行net(X)时，模型将自动推断出每一层的输入个数。我们将在第4章详细介绍这种机制。Gluon 的这一设计为模型开发带来便利。
在使用net前，我们需要初始化模型参数，如线性回归模型中的权重和偏差。我们从 MXNet 导入init模块。该模块提供了模型参数初始化的各种方法。这里的init是initializer的缩写形式。我们通过init.Normal(sigma=0.01)指定权重参数每个元素将在初始化时随机采样于均值为0、标准差为 0.01 的正态分布。偏差参数默认会初始化为零。
In [6]: from mxnet import init
net.initialize(init.Normal(sigma=0.01))在 Gluon 中，loss模块定义了各种损失函数。我们用假名gloss代替导入的loss模块，并直接使用它提供的平方损失作为模型的损失函数。
In [7]: from mxnet.gluon import loss as gloss
loss = gloss.L2Loss() # 平方损失又称L2范数损失同样，我们也无须实现小批量随机梯度下降。在导入 Gluon 后，我们创建一个Trainer实例，并指定学习率为 0.03 的小批量随机梯度下降（sgd）为优化算法。该优化算法将用来迭代net实例所有通过add函数嵌套的层所包含的全部参数。这些参数可以通过collect_params函数获取。
In [8]: from mxnet import gluon
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.03})在使用 Gluon 训练模型时，我们通过调用Trainer实例的step函数来迭代模型参数。3.2节中我们提到，由于变量l是长度为batch_size的一维 NDArray，执行l.backward()等价于执行l.sum().backward()。按照小批量随机梯度下降的定义，我们在step函数中指明批量大小，从而对批量中样本梯度求平均。
In [9]: num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
with autograd.record():
l = loss(net(X), y)
l.backward()
trainer.step(batch_size)
l = loss(net(features), labels)
print('epoch %d, loss: %f' % (epoch, l.mean().asnumpy()))
epoch 1, loss: 0.040309
epoch 2, loss: 0.000153
epoch 3, loss: 0.000050下面我们分别比较学到的模型参数和真实的模型参数。我们从net获得需要的层，并访问其权重（weight）和偏差（bias）。学到的模型参数和真实的参数很接近。
In [10]: dense = net[0]
true_w, dense.weight.data()
Out[10]: ([2, -3.4],
[[ 1.9996833 -3.3997345]]
<NDArray 1x2 @cpu(0)>)
In [11]: true_b, dense.bias.data()
Out[11]: (4.2,
[4.1996784]
<NDArray 1 @cpu(0)>)小结
- 使用 Gluon 可以更简洁地实现模型。
- 在 Gluon 中，
data模块提供了有关数据处理的工具，nn模块定义了大量神经网络的层，loss模块定义了各种损失函数。- MXNet 的
initializer模块提供了模型参数初始化的各种方法。练习
（1）如果将
l = loss(net(X), y)替换成l = loss(net(X), y).mean()，我们需要将trainer.step(batch_size)相应地改成trainer.step(1)。这是为什么呢？（2）查阅 MXNet 文档，看看
gluon.loss和init模块里提供了哪些损失函数和初始化方法。（3）如何访问
dense.weight的梯度？
扫码直达讨论区
前几节介绍的线性回归模型适用于输出为连续值的情景。在另一类情景中，模型输出可以是一个像图像类别这样的离散值。对于这样的离散值预测问题，我们可以使用诸如 softmax回归在内的分类模型。和线性回归不同，softmax 回归的输出单元从一个变成了多个，且引入了 softmax 运算使输出更适合离散值的预测和训练。本节以 softmax 回归模型为例，介绍神经网络中的分类模型。
让我们考虑一个简单的图像分类问题，其输入图像的高和宽均为2像素，且色彩为灰度。这样每个像素值都可以用一个标量表示。我们将图像中的4像素分别记为
。假设训练数据集中图像的真实标签为狗、猫或鸡（假设可以用 4像素表示出这3种动物），这些标签分别对应离散值
。
我们通常使用离散的数值来表示类别，例如
。如此，一张图像的标签为 1、2 和 3 这3个数值中的一个。虽然我们仍然可以使用回归模型来进行建模，并将预测值就近定点化到 1、2 和 3 这3个离散值之一，但这种连续值到离散值的转化通常会影响到分类质量。因此我们一般使用更加适合离散值输出的模型来解决分类问题。
softmax 回归和线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于，softmax 回归的输出值个数等于标签里的类别数。因为一共有 4 种特征和 3 种输出动物类别，所以权重包含12 个标量（带下标的w）、偏差包含 3 个标量（带下标的b），且对每个输入计算
这3个输出：
图3-2用神经网络图描绘了上面的计算。softmax 回归同线性回归一样，也是一个单层神经网络。由于每个输出
的计算都要依赖于所有的输入
，softmax 回归的输出层也是一个全连接层。
图3-2 softmax回归是一个单层神经网络
既然分类问题需要得到离散的预测输出，一个简单的办法是将输出值
当作预测类别是i 的置信度，并将值最大的输出所对应的类作为预测输出，即输出
。例如，如果
分别为
，由于
最大，那么预测类别为2，其代表猫。
然而，直接使用输出层的输出有两个问题。一方面，由于输出层的输出值的范围不确定，我们难以直观上判断这些值的意义。例如，刚才举的例子中的输出值 10 表示“很置信”图像类别为猫，因为该输出值是其他两类的输出值的 100 倍。但如果
，那么输出值 10 却又表示图像类别为猫的概率很低。另一方面，由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。
softmax 运算解决了以上两个问题。它通过下式将输出值变换成值为正且和为 1 的概率分布：
其中
容易看出
且
，因此
是一个合法的概率分布。这时候，如果
，不管
和
的值是多少，我们都知道图像类别为猫的概率是 80%。此外，我们注意到
因此 softmax 运算不改变预测类别输出。
为了提高计算效率，我们可以将单样本分类通过矢量计算来表达。在上面的图像分类问题中，假设 softmax 回归的权重和偏差参数分别为
设高和宽分别为 2 个像素的图像样本i的特征为
输出层的输出为
预测为狗、猫或鸡的概率分布为
softmax 回归对样本i分类的矢量计算表达式为
为了进一步提升计算效率，我们通常对小批量数据做矢量计算。广义上讲，给定一个小批量样本，其批量大小为 n，输入个数（特征数）为d，输出个数（类别数）为q。设批量特征为
。假设 softmax 回归的权重和偏差参数分别为
和
。softmax 回归的矢量计算表达式为
其中的加法运算使用了广播机制，
且这两个矩阵的第 i行分别为样本i的输出 
和概率分布
。
前面提到，使用 softmax 运算后可以更方便地与离散标签计算误差。我们已经知道，softmax 运算将输出变换成一个合法的类别预测分布。实际上，真实标签也可以用类别分布表达：对于样本i，我们构造向量
，使其第
（样本i 类别的离散数值）个元素为1，其余为0。这样我们的训练目标可以设为使预测概率分布
尽可能接近真实的标签概率分布。
我们可以像线性回归那样使用平方损失函数
。然而，想要预测分类结果正确，我们其实并不需要预测概率完全等于标签概率。例如，在图像分类的例子里，如果
，那么我们只需要
比其他两个预测值
和
大就行了。即使值为 0.6，不管其他两个预测值为多少，类别预测均正确。而平方损失则过于严格，例如
比
的损失要小很多，虽然两者都有同样正确的分类预测结果。
改善上述问题的一个方法是使用更适合衡量两个概率分布差异的测量函数。其中，交叉熵（cross entropy）是一个常用的衡量方法：
其中带下标的
是向量
中非 0 即 1 的元素，需要注意将它与样本i 类别的离散数值，即不带下标的区分。在上式中，我们知道向量中只有第个元素
为 1，其余全为0，于是
。也就是说，交叉熵只关心对正确类别的预测概率，因为只要其值
足够大，就可以确保分类结果正确。当然，遇到一个样本有多个标签时，例如图像里含有不止一个物体时，我们并不能做这一步简化。但即便对于这种情况，交叉熵同样只关心对图像中出现的物体类别的预测概率。
假设训练数据集的样本数为n，交叉熵损失函数定义为
其中
代表模型参数。同样地，如果每个样本只有一个标签，那么交叉熵损失可以简写成
。从另一个角度来看，我们知道最小化
等价于最大化
，即最小化交叉熵损失函数等价于最大化训练数据集所有标签类别的联合预测概率。
在训练好 softmax 回归模型后，给定任一样本特征，就可以预测每个输出类别的概率。通常，我们把预测概率最大的类别作为输出类别。如果它与真实类别（标签）一致，说明这次预测是正确的。在3.6节的实验中，我们将使用准确率（accuracy）来评价模型的表现。它等于正确预测数量与总预测数量之比。
小结
- softmax 回归适用于分类问题。它使用 softmax 运算输出类别的概率分布。
- softmax 回归是一个单层神经网络，输出个数等于分类问题中的类别个数。
- 交叉熵适合衡量两个概率分布的差异。
练习
查阅资料，了解最大似然估计。它与最小化交叉熵损失函数有哪些异曲同工之妙？
扫码直达讨论区
在介绍 softmax 回归的实现前我们先引入一个多类图像分类数据集。它将在后面的章节中被多次使用，以方便我们观察比较算法之间在模型精度和计算效率上的区别。图像分类数据集中最常用的是手写数字识别数据集MNIST。但大部分模型在 MNIST 上的分类精度都超过了 95%。为了更直观地观察算法之间的差异，我们将使用一个图像内容更加复杂的Fashion-MNIST数据集[60]。
首先导入本节需要的包或模块。
In [1]: %matplotlib inline
import d2lzh as d2l
from mxnet.gluon import data as gdata
import sys
import time下面，我们通过 Gluon 的data包来下载这个数据集。第一次调用时会自动从网上获取数据。我们通过参数train来指定获取训练数据集或测试数据集（testing data set）。测试数据集也叫测试集（testing set），只用来评价模型的表现，并不用来训练模型。
In [2]: mnist_train = gdata.vision.FashionMNIST(train=True)
mnist_test = gdata.vision.FashionMNIST(train=False)训练集中和测试集中的每个类别的图像数分别为 6 000 和 1 000。因为有 10 个类别，所以训练集和测试集的样本数分别为 60 000 和 10 000。
In [3]: len(mnist_train), len(mnist_test)
Out[3]: (60000, 10000)我们可以通过方括号[]来访问任意一个样本，下面获取第一个样本的图像和标签。
In [4]: feature, label = mnist_train[0]变量feature对应高和宽均为 28 像素的图像。每个像素的数值为 0 到 255 之间 8 位无符号整数（uint8）。它使用三维的 NDArray存储，其中的最后一维是通道数。因为数据集中是灰度图像，所以通道数为1。为了表述简洁，我们将高和宽分别为h和w像素的图像的形状记为
或(h, w)。
In [5]: feature.shape, feature.dtype
Out[5]: ((28, 28, 1), numpy.uint8)图像的标签使用 NumPy 的标量表示。它的类型为 32 位整数（int32）。
In [6]: label, type(label), label.dtype
Out[6]: (2, numpy.int32, dtype('int32'))Fashion-MNIST 中一共包括了 10 个类别，分别为t-shirt（T 恤）、trouser（裤子）、pullover（套衫）、dress（连衣裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和 ankle boot（短靴）。以下函数可以将数值标签转成相应的文本标签。
In [7]: # 本函数已保存在d2lzh包中方便以后使用
def get_fashion_mnist_labels(labels):
text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
return [text_labels[int(i)] for i in labels]下面定义一个可以在一行里画出多张图像和对应标签的函数。
In [8]: # 本函数已保存在d2lzh包中方便以后使用
def show_fashion_mnist(images, labels):
d2l.use_svg_display()
# 这里的_表示我们忽略（不使用）的变量
_, f igs = d2l.plt.subplots(1, len(images), f igsize=(12, 12))
for f, img, lbl in zip(f igs, images, labels):
f.imshow(img.reshape((28, 28)).asnumpy())
f.set_title(lbl)
f.axes.get_xaxis().set_visible(False)
f.axes.get_yaxis().set_visible(False)现在，我们看一下训练数据集中前 9 个样本的图像内容和文本标签。
In [9]: X, y = mnist_train[0:9]
show_fashion_mnist(X, get_fashion_mnist_labels(y))我们将在训练数据集上训练模型，并将训练好的模型在测试数据集上评价模型的表现。虽然我们可以像3.2节中那样通过yield来定义读取小批量数据样本的函数，但为了代码简洁，这里我们直接创建DataLoader实例。该实例每次读取一个样本数为batch_size的小批量数据。这里的批量大小batch_size是一个超参数。
在实践中，数据读取经常是训练的性能瓶颈，特别当模型较简单或者计算硬件性能较高时。Gluon 的DataLoader中一个很方便的功能是允许使用多进程来加速数据读取（暂不支持 Windows 操作系统）。这里我们通过参数num_workers来设置 4 个进程读取数据。
此外，我们通过ToTensor实例将图像数据从 uint8格式变换成 32 位浮点数格式，并除以 255 使得所有像素的数值均在 0 到 1 之间。ToTensor实例还将图像通道从最后一维移到最前一维来方便之后介绍的卷积神经网络计算。通过数据集的transform_f irst函数，我们将ToTensor的变换应用在每个数据样本（图像和标签）的第一个元素，即图像之上。
In [10]: batch_size = 256
transformer = gdata.vision.transforms.ToTensor()
if sys.platform.startswith('win'):
num_workers = 0 # 0表示不用额外的进程来加速读取数据
else:
num_workers = 4
train_iter = gdata.DataLoader(mnist_train.transform_f irst(transformer),
batch_size, shuff le=True,
num_workers=num_workers)
test_iter = gdata.DataLoader(mnist_test.transform_f irst(transformer),
batch_size, shuff le=False,
num_workers=num_workers)我们将获取并读取 Fashion-MNIST 数据集的逻辑封装在d2lzh.load_data_fashion_mnist函数中供后面章节调用。该函数将返回train_iter和test_iter两个变量。随着本书内容的不断深入，我们会进一步改进该函数。它的完整实现将在5.6节中描述。
最后我们查看读取一遍训练数据需要的时间。
In [11]: start = time.time()
for X, y in train_iter:
continue
'%.2f sec' % (time.time() - start)
Out[11]: '1.26 sec'小结
- Fashion-MNIST 是一个 10 类服饰分类数据集，之后章节里将使用它来检验不同算法的表现。
- 我们将高和宽分别为h和w像素的图像的形状记为
练习
（1）减小
batch_size（如到1）会影响读取性能吗？（2）非 Windows 用户请尝试修改
num_workers来查看它对读取性能的影响。（3）查阅 MXNet 文档，
mxnet.gluon.data.vision里还提供了哪些别的数据集？（4）查阅 MXNet 文档，
mxnet.gluon.data.vision.transforms还提供了哪些别的变换方法？
扫码直达讨论区
这一节我们来动手实现 softmax 回归。首先导入本节实现所需的包或模块。
In [1]: %matplotlib inline
import d2lzh as d2l
from mxnet import autograd, nd我们将使用 Fashion-MNIST 数据集，并设置批量大小为 256。
In [2]: batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)跟线性回归中的例子一样，我们将使用向量表示每个样本。已知每个样本输入是高和宽均为 28 像素的图像。模型的输入向量的长度是28×28=784：该向量的每个元素对应图像中每个像素。由于图像有 10 个类别，单层神经网络输出层的输出个数为 10，因此softmax 回归的权重和偏差参数分别为 784×10 和1×10 的矩阵。
In [3]: num_inputs = 784
num_outputs = 10
W = nd.random.normal(scale=0.01, shape=(num_inputs, num_outputs))
b = nd.zeros(num_outputs)同之前一样，我们要为模型参数附上梯度。
In [4]: W.attach_grad()
b.attach_grad()在介绍如何定义 softmax 回归之前，我们先描述一下对如何对多维 NDArray 按维度操作。在下面的例子中，给定一个 NDArray矩阵X，我们可以只对其中同一列（axis=0）或同一行（axis=1）的元素求和，并在结果中保留行和列这两个维度（keepdims=True）。
In [5]: X = nd.array([[1, 2, 3], [4, 5, 6]])
X.sum(axis=0, keepdims=True), X.sum(axis=1, keepdims=True)
Out[5]: (
[[5. 7. 9.]]
<NDArray 1x3 @cpu(0)>,
[[ 6.]
[15.]]
<NDArray 2x1 @cpu(0)>)下面我们就可以定义3.4节介绍的 softmax 运算了。在下面的函数中，矩阵X的行数是样本数，列数是输出个数。为了表达样本预测各个输出的概率，softmax 运算会先通过exp函数对每个元素做指数运算，再对exp矩阵同行元素求和，最后令矩阵每行各元素与该行元素之和相除。这样一来，最终得到的矩阵每行元素和为 1 且非负。因此，该矩阵每行都是合法的概率分布。softmax 运算的输出矩阵中的任意一行元素代表了一个样本在各个输出类别上的预测概率。
In [6]: def softmax(X):
X_exp = X.exp()
partition = X_exp.sum(axis=1, keepdims=True)
return X_exp / partition # 这里应用了广播机制可以看到，对于随机输入，我们将每个元素变成了非负数，且每一行和为 1。
In [7]: X = nd.random.normal(shape=(2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(axis=1)
Out[7]: (
[[0.21324193 0.33961776 0.1239742 0.27106097 0.05210521]
[0.11462264 0.3461234 0.19401033 0.29583326 0.04941036]]
<NDArray 2x5 @cpu(0)>,
[1.0000001 1. ]
<NDArray 2 @cpu(0)>)有了 softmax 运算，我们可以定义3.4节描述的 softmax 回归模型了。这里通过reshape函数将每张原始图像改成长度为num_inputs的向量。
In [8]: def net(X):
return softmax(nd.dot(X.reshape((-1, num_inputs)), W) + b)在3.4节中，我们介绍了 softmax 回归使用的交叉熵损失函数。为了得到标签的预测概率，我们可以使用pick函数。在下面的例子中，变量y_hat是 2 个样本在 3 个类别的预测概率，变量y是这 2 个样本的标签类别。通过使用pick函数，我们得到了 2 个样本的标签的预测概率。与3.4节数学表述中标签类别离散值从 1 开始逐一递增不同，在代码中，标签类别的离散值是从 0 开始逐一递增的。
In [9]: y_hat = nd.array([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y = nd.array([0, 2], dtype='int32')
nd.pick(y_hat, y)
Out[9]:
[0.1 0.5]
<NDArray 2 @cpu(0)>下面实现了3.4节中介绍的交叉熵损失函数。
In [10]: def cross_entropy(y_hat, y):
return -nd.pick(y_hat, y).log()给定一个类别的预测概率分布y_hat，我们把预测概率最大的类别作为输出类别。如果它与真实类别y一致，说明这次预测是正确的。分类准确率即正确预测数量与总预测数量之比。
为了演示准确率的计算，下面定义准确率accuracy函数。其中y_hat.argmax(axis=1)返回矩阵y_hat每行中最大元素的索引，且返回结果与变量y形状相同。我们在2.2节介绍过，相等条件判别式(y_hat.argmax(axis=1) == y)是一个值为 0（相等为假）或 1（相等为真）的NDArray。由于标签类型为整数，我们先将变量y变换为浮点数再进行相等条件判断。
In [11]: def accuracy(y_hat, y):
return (y_hat.argmax(axis=1) == y.astype('f loat32')).mean().asscalar()让我们继续使用在演示pick函数时定义的变量y_hat和y，并将它们分别作为预测概率分布和标签。可以看到，第一个样本预测类别为 2（该行最大元素 0.6 在本行的索引为 2），与真实标签 0 不一致；第二个样本预测类别为 2（该行最大元素 0.5 在本行的索引为 2），与真实标签 2 一致。因此，这两个样本上的分类准确率为 0.5。
In [12]: accuracy(y_hat, y)
Out[12]: 0.5类似地，我们可以评价模型net在数据集data_iter上的准确率。
In [13]: # 本函数已保存在d2lzh包中方便以后使用。该函数将被逐步改进：它的完整实现将在9.1节中描述
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
y = y.astype('f loat32')
acc_sum += (net(X).argmax(axis=1) == y).sum().asscalar()
n += y.size
return acc_sum / n 因为我们随机初始化了模型net，所以这个随机模型的准确率应该接近于类别个数 10 的倒数 0.1。
In [14]: evaluate_accuracy(test_iter, net)
Out[14]: 0.0925训练 softmax 回归的实现与3.2节介绍的线性回归中的实现非常相似。我们同样使用小批量随机梯度下降来优化模型的损失函数。在训练模型时，迭代周期数num_epochs和学习率lr都是可以调的超参数。改变它们的值可能会得到分类更准确的模型。
In [15]: num_epochs, lr = 5, 0.1
# 本函数已保存在d2lzh包中方便以后使用
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params=None, lr=None, trainer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
with autograd.record():
y_hat = net(X)
l = loss(y_hat, y).sum()
l.backward()
if trainer is None:
d2l.sgd(params, lr, batch_size)
else:
trainer.step(batch_size) # 3.7节将用到
y = y.astype('f loat32')
train_l_sum += l.asscalar()
train_acc_sum += (y_hat.argmax(axis=1) == y).sum().asscalar()
n += y.size
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size,
[W, b], lr)
epoch 1, loss 0.7882, train acc 0.749, test acc 0.800
epoch 2, loss 0.5741, train acc 0.811, test acc 0.824
epoch 3, loss 0.5298, train acc 0.823, test acc 0.830
epoch 4, loss 0.5055, train acc 0.830, test acc 0.834
epoch 5, loss 0.4887, train acc 0.834, test acc 0.840训练完成后，现在就可以演示如何对图像进行分类了。给定一系列图像（第三行图像输出），我们比较一下它们的真实标签（第一行文本输出）和模型预测结果（第二行文本输出）。
In [16]: for X, y in test_iter:
break
true_labels = d2l.get_fashion_mnist_labels(y.asnumpy())
pred_labels = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1).asnumpy())
titles = [true + '\n' + pred for true, pred in zip(true_labels, pred_labels)]
d2l.show_fashion_mnist(X[0:9], titles[0:9])小结
- 可以使用 softmax 回归做多类别分类。与训练线性回归相比，你会发现训练 softmax 回归的步骤和它非常相似：获取并读取数据、定义模型和损失函数并使用优化算法训练模型。事实上，绝大多数深度学习模型的训练都有着类似的步骤。
练习
（1）在本节中，我们直接按照 softmax 运算的数学定义来实现 softmax 函数。这可能会造成什么问题？（提示：试一试计算exp(50)的大小。）
（2）本节中的
cross_entropy函数是按照3.4节中的交叉熵损失函数的数学定义实现的。这样的实现方式可能有什么问题？（提示：思考一下对数函数的定义域。）（3）你能想到哪些办法来解决上面的两个问题？
扫码直达讨论区
我们在3.3节中已经了解了使用 Gluon 实现模型的便利。下面，让我们再次使用 Gluon 来实现一个 softmax 回归模型。首先导入所需的包或模块。
In [1]: %matplotlib inline
import d2lzh as d2l
from mxnet import gluon, init
from mxnet.gluon import loss as gloss, nn我们仍然使用 Fashion-MNIST 数据集和3.6节中设置的批量大小。
In [2]: batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)在3.4节中提到，softmax 回归的输出层是一个全连接层。因此，我们添加一个输出个数为 10 的全连接层。我们使用均值为 0、标准差为 0.01 的正态分布随机初始化模型的权重参数。
In [3]: net = nn.Sequential()
net.add(nn.Dense(10))
net.initialize(init.Normal(sigma=0.01))如果做了3.6节的练习，那么你可能意识到了分开定义 softmax 运算和交叉熵损失函数可能会造成数值不稳定。因此，Gluon 提供了一个包括 softmax 运算和交叉熵损失计算的函数。它的数值稳定性更好。
In [4]: loss = gloss.SoftmaxCrossEntropyLoss()我们使用学习率为 0.1 的小批量随机梯度下降作为优化算法。
In [5]: trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.1})接下来，我们使用3.6节中定义的训练函数来训练模型。
In [6]: num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None,
None, trainer)
epoch 1, loss 0.7885, train acc 0.747, test acc 0.806
epoch 2, loss 0.5741, train acc 0.811, test acc 0.824
epoch 3, loss 0.5293, train acc 0.824, test acc 0.832
epoch 4, loss 0.5042, train acc 0.831, test acc 0.838
epoch 5, loss 0.4892, train acc 0.835, test acc 0.841小结
Gluon 提供的函数往往具有更好的数值稳定性。
可以使用 Gluon 更简洁地实现 softmax 回归。
练习
尝试调一调超参数，如批量大小、迭代周期和学习率，看看结果会怎样。
扫码直达讨论区
我们已经介绍了包括线性回归和 softmax 回归在内的单层神经网络。然而深度学习主要关注多层模型。在本节中，我们将以多层感知机（multilayer perceptron，MLP）为例，介绍多层神经网络的概念。
多层感知机在单层神经网络的基础上引入了一到多个隐藏层（hidden layer）。隐藏层位于输入层和输出层之间。图3-3展示了一个多层感知机的神经网络图。
图3-3 带有隐藏层的多层感知机。它含有一个隐藏层，该层中有 5 个隐藏单元
在图3-3所示的多层感知机中，输入和输出个数分别为 4 和 3，中间的隐藏层中包含了 5 个隐藏单元（hidden unit）。由于输入层不涉及计算，图3-3 中的多层感知机的层数为 2。由图3-3 可见，隐藏层中的神经元和输入层中各个输入完全连接，输出层中的神经元和隐藏层中的各个神经元也完全连接。因此，多层感知机中的隐藏层和输出层都是全连接层。
具体来说，给定一个小批量样本
，其批量大小为 n，输入个数为d。假设多层感知机只有一个隐藏层，其中隐藏单元个数为h。记隐藏层的输出（也称为隐藏层变量或隐藏变量）为
，有
。因为隐藏层和输出层均是全连接层，可以设隐藏层的权重参数和偏差参数分别为
和
，输出层的权重和偏差参数分别为
和
。
我们先来看一种含单隐藏层的多层感知机的设计。其输出
的计算为
也就是将隐藏层的输出直接作为输出层的输入。如果将以上两个式子联立起来，可以得到
从联立后的式子可以看出，虽然神经网络引入了隐藏层，却依然等价于一个单层神经网络：其中输出层权重参数为
，偏差参数为
。不难发现，即便再添加更多的隐藏层，以上设计依然只能与仅含输出层的单层神经网络等价。
上述问题的根源在于全连接层只是对数据做仿射变换（aff ine transformation），而多个仿射变换的叠加仍然是一个仿射变换。解决问题的一个方法是引入非线性变换，例如对隐藏变量使用按元素运算的非线性函数进行变换，然后再作为下一个全连接层的输入。这个非线性函数被称为激活函数（activation function）。下面我们介绍几个常用的激活函数。
ReLU（rectif ied linear unit）函数提供了一个很简单的非线性变换。给定元素x，该函数定义为
可以看出，ReLU函数只保留正数元素，并将负数元素清零。为了直观地观察这一非线性变换，我们先定义一个绘图函数xyplot。
In [1]: %matplotlib inline
import d2lzh as d2l
from mxnet import autograd, nd
def xyplot(x_vals, y_vals, name):
d2l.set_f igsize(f igsize=(5, 2.5))
d2l.plt.plot(x_vals.asnumpy(), y_vals.asnumpy())
d2l.plt.xlabel('x')
d2l.plt.ylabel(name + '(x)')我们接下来通过NDArray提供的relu函数来绘制 ReLU 函数。可以看到，该激活函数是一个两段线性函数。
In [2]: x = nd.arange(-8.0, 8.0, 0.1)
x.attach_grad()
with autograd.record():
y = x.relu()
xyplot(x, y, 'relu')显然，当输入为负数时，ReLU 函数的导数为 0；当输入为正数时，ReLU 函数的导数为 1。尽管输入为 0 时 ReLU 函数不可导，但是我们可以取此处的导数为 0。下面绘制ReLU 函数的导数。
In [3]: y.backward()
xyplot(x, x.grad, 'grad of relu')sigmoid函数可以将元素的值变换到0和1之间：
sigmoid 函数在早期的神经网络中较为普遍，但它目前逐渐被更简单的 ReLU 函数取代。在第6章中我们会介绍如何利用它值域在 0 到 1 之间这一特性来控制信息在神经网络中的流动。下面绘制了 sigmoid 函数。当输入接近 0 时，sigmoid 函数接近线性变换。
In [4]: with autograd.record():
y = x.sigmoid()
xyplot(x, y, 'sigmoid')依据链式法则，sigmoid 函数的导数为
下面绘制了 sigmoid 函数的导数。当输入为 0 时，sigmoid 函数的导数达到最大值 0.25；当输入越偏离 0 时，sigmoid 函数的导数越接近 0。
In [5]: y.backward()
xyplot(x, x.grad, 'grad of sigmoid')tanh（双曲正切）函数可以将元素的值变换到 -1 和 1 之间：
我们接着绘制 tanh函数。当输入接近 0 时，tanh 函数接近线性变换。虽然该函数的形状和 sigmoid 函数的形状很像，但 tanh 函数在坐标系的原点上对称。
In [6]: with autograd.record():
y = x.tanh()
xyplot(x, y, 'tanh')依据链式法则，tanh 函数的导数为
下面绘制了 tanh 函数的导数。当输入为 0 时，tanh 函数的导数达到最大值 1；当输入越偏离 0 时，tanh 函数的导数越接近 0。
In [7]: y.backward()
xyplot(x, x.grad, 'grad of tanh')多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络，且每个隐藏层的输出通过激活函数进行变换。多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例并沿用本节之前定义的符号，多层感知机按以下方式计算输出：
其中φ表示激活函数。在分类问题中，我们可以对输出O 做softmax 运算，并使用 softmax 回归中的交叉熵损失函数。在回归问题中，我们将输出层的输出个数设为1，并将输出O 直接提供给线性回归中使用的平方损失函数。
小结
- 多层感知机在输出层与输入层之间加入了一个或多个全连接隐藏层，并通过激活函数对隐藏层输出进行变换。
- 常用的激活函数包括 ReLU 函数、sigmoid 函数和 tanh 函数。
练习
（1）应用链式法则，推导出 sigmoid 函数和 tanh 函数的导数的数学表达式。
（2）查阅资料，了解其他的激活函数。
扫码直达讨论区
我们已经从3.8节里了解了多层感知机的原理。下面，我们一起来动手实现一个多层感知机。首先导入实现所需的包或模块。
In [1]: %matplotlib inline
import d2lzh as d2l
from mxnet import nd
from mxnet.gluon import loss as gloss这里继续使用 Fashion-MNIST 数据集。我们将使用多层感知机对图像进行分类。
In [2]: batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)我们在3.5节里已经介绍了，Fashion-MNIST 数据集中图像形状为28×28，类别数为 10。本节中我们依然使用长度为28×28=784 的向量表示每一张图像。因此，输入个数为784，输出个数为10。实验中，我们设超参数隐藏单元个数为256。
In [3]: num_inputs, num_outputs, num_hiddens = 784, 10, 256
W1 = nd.random.normal(scale=0.01, shape=(num_inputs, num_hiddens))
b1 = nd.zeros(num_hiddens)
W2 = nd.random.normal(scale=0.01, shape=(num_hiddens, num_outputs))
b2 = nd.zeros(num_outputs)
params = [W1, b1, W2, b2]
for param in params:
param.attach_grad()这里我们使用基础的maximum函数来实现 ReLU，而非直接调用MXNet的relu函数。
In [4]: def relu(X):
return nd.maximum(X, 0)同 softmax 回归一样，我们通过reshape函数将每张原始图像改成长度为num_inputs的向量。然后我们实现3.8节中多层感知机的计算表达式。
In [5]: def net(X):
X = X.reshape((-1, num_inputs))
H = relu(nd.dot(X, W1) + b1)
return nd.dot(H, W2) + b2为了得到更好的数值稳定性，我们直接使用 Gluon 提供的包括 softmax 运算和交叉熵损失计算的函数。
In [6]: loss = gloss.SoftmaxCrossEntropyLoss()训练多层感知机的步骤和3.6节中训练 softmax 回归的步骤没什么区别。我们直接调用d2lzh包中的train_ch3函数，它的实现已经在3.6节里介绍过。我们在这里设超参数迭代周期数为 5，学习率为 0.5。
In [7]: num_epochs, lr = 5, 0.5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params, lr)
epoch 1, loss 0.7941, train acc 0.704, test acc 0.817
epoch 2, loss 0.4859, train acc 0.821, test acc 0.846
epoch 3, loss 0.4289, train acc 0.840, test acc 0.864
epoch 4, loss 0.3949, train acc 0.855, test acc 0.867
epoch 5, loss 0.3717, train acc 0.863, test acc 0.873小结
可以通过手动定义模型及其参数来实现简单的多层感知机。
当多层感知机的层数较多时，本节的实现方法会显得较烦琐，如在定义模型参数的时候。
练习
（1）改变超参数
num_hiddens的值，看看对实验结果有什么影响。（2）试着加入一个新的隐藏层，看看对实验结果有什么影响。
扫码直达讨论区
下面我们使用 Gluon 来实现3.9节中的多层感知机。首先导入所需的包或模块。
In [1]: import d2lzh as d2l
from mxnet import gluon, init
from mxnet.gluon import loss as gloss, nn和 softmax 回归唯一的不同在于，我们多加了一个全连接层作为隐藏层。它的隐藏单元个数为 256，并使用 ReLU 函数作为激活函数。
In [2]: net = nn.Sequential()
net.add(nn.Dense(256, activation='relu'),
nn.Dense(10))
net.initialize(init.Normal(sigma=0.01))我们使用与3.7节中训练 softmax 回归几乎相同的步骤来读取数据并训练模型。
In [3]: batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
loss = gloss.SoftmaxCrossEntropyLoss()
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': 0.5})
num_epochs = 5
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None,
None, trainer)
epoch 1, loss 0.8033, train acc 0.701, test acc 0.819
epoch 2, loss 0.4998, train acc 0.815, test acc 0.836
epoch 3, loss 0.4332, train acc 0.838, test acc 0.862
epoch 4, loss 0.4019, train acc 0.851, test acc 0.855
epoch 5, loss 0.3755, train acc 0.862, test acc 0.873小结
- 通过 Gluon可以更简洁地实现多层感知机。
练习
（1）尝试多加入几个隐藏层，对比3.9节中从零开始的实现。
（2）使用其他的激活函数，看看对结果的影响。
扫码直达讨论区
在前几节基于 Fashion-MNIST 数据集的实验中，我们评价了机器学习模型在训练数据集和测试数据集上的表现。如果你改变过实验中的模型结构或者超参数，你也许发现了：当模型在训练数据集上更准确时，它在测试数据集上却不一定更准确。这是为什么呢？
在解释上述现象之前，我们需要区分训练误差（training error）和泛化误差（generalization error）。通俗来讲，前者指模型在训练数据集上表现出的误差，后者指模型在任意一个测试数据样本上表现出的误差的期望，并常常通过测试数据集上的误差来近似。计算训练误差和泛化误差可以使用之前介绍过的损失函数，例如线性回归用到的平方损失函数和 softmax 回归用到的交叉熵损失函数。
让我们以高考为例来直观地解释训练误差和泛化误差这两个概念。训练误差可以认为是做往年高考试题（训练题）时的错误率，泛化误差则可以通过真正参加高考（测试题）时的答题错误率来近似。假设训练题和测试题都随机采样于一个未知的依照相同考纲的巨大试题库。如果让一名未学习中学知识的小学生去答题，那么测试题和训练题的答题错误率可能很相近。但如果换成一名反复练习训练题的高三备考生答题，即使在训练题上做到了错误率为 0，也不代表真实的高考成绩会如此。
在机器学习里，我们通常假设训练数据集（训练题）和测试数据集（测试题）里的每一个样本都是从同一个概率分布中相互独立地生成的。基于该独立同分布假设，给定任意一个机器学习模型（含参数），它的训练误差的期望和泛化误差都是一样的。例如，如果我们将模型参数设成随机值（小学生），那么训练误差和泛化误差会非常相近。但我们从前面几节中已经了解到，模型的参数是通过在训练数据集上训练模型而学习出的，参数的选择依据了最小化训练误差（高三备考生）。所以，训练误差的期望小于或等于泛化误差。也就是说，一般情况下，由训练数据集学到的模型参数会使模型在训练数据集上的表现优于或等于在测试数据集上的表现。由于无法从训练误差估计泛化误差，一味地降低训练误差并不意味着泛化误差一定会降低。
机器学习模型应关注降低泛化误差。
在机器学习中，通常需要评估若干候选模型的表现并从中选择模型。这一过程称为模型选择（model selection）。可供选择的候选模型可以是有着不同超参数的同类模型。以多层感知机为例，我们可以选择隐藏层的个数，以及每个隐藏层中隐藏单元个数和激活函数。为了得到有效的模型，我们通常要在模型选择上下一番功夫。下面，我们来描述模型选择中经常使用的验证数据集（validation data set）。
从严格意义上讲，测试集只能在所有超参数和模型参数选定后使用一次。不可以使用测试数据选择模型，如调参。由于无法从训练误差估计泛化误差，因此也不应只依赖训练数据选择模型。鉴于此，我们可以预留一部分在训练数据集和测试数据集以外的数据来进行模型选择。这部分数据被称为验证数据集，简称验证集（validation set）。例如，我们可以从给定的训练集中随机选取一小部分作为验证集，而将剩余部分作为真正的训练集。
然而在实际应用中，由于数据不容易获取，测试数据极少只使用一次就丢弃。因此，实践中验证数据集和测试数据集的界限可能比较模糊。从严格意义上讲，除非明确说明，否则本书中实验所使用的测试集应为验证集，实验报告的测试结果（如测试准确率）应为验证结果（如验证准确率）。
由于验证数据集不参与模型训练，当训练数据不够用时，预留大量的验证数据显得太奢侈。一种改善的方法是k折交叉验证（k-fold cross-validation）。在k折交叉验证中，我们把原始训练数据集分割成 k 个不重合的子数据集，然后我们做k次模型训练和验证。每一次，我们使用一个子数据集验证模型，并使用其他k-1个子数据集来训练模型。在这k 次训练和验证中，每次用来验证模型的子数据集都不同。最后，我们对这k次训练误差和验证误差分别求平均。
接下来，我们将探究模型训练中经常出现的两类典型问题：一类是模型无法得到较低的训练误差，我们将这一现象称作欠拟合（underf itting）；另一类是模型的训练误差远小于它在测试数据集上的误差，我们称该现象为过拟合（overf itting）。在实践中，我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题，在这里我们重点讨论两个因素：模型复杂度和训练数据集大小。
为了解释模型复杂度，我们以多项式函数拟合为例。给定一个由标量数据特征x和对应的标量标签y 组成的训练数据集，多项式函数拟合的目标是找一个K阶多项式函数
来近似y。在上式中，
是模型的权重参数，b 是偏差参数。与线性回归相同，多项式函数拟合也使用平方损失函数。特别地，一阶多项式函数拟合又叫线性函数拟合。
因为高阶多项式函数模型参数更多，模型函数的选择空间更大，所以高阶多项式函数比低阶多项式函数的复杂度更高。因此，高阶多项式函数比低阶多项式函数更容易在相同的训练数据集上得到更低的训练误差。给定训练数据集，模型复杂度和误差之间的关系通常如图3-4所示。给定训练数据集，如果模型的复杂度过低，很容易出现欠拟合；如果模型复杂度过高，很容易出现过拟合。应对欠拟合和过拟合的一个办法是针对数据集选择合适复杂度的模型。
影响欠拟合和过拟合的另一个重要因素是训练数据集的大小。一般来说，如果训练数据集中样本数过少，特别是比模型参数数量（按元素计）更少时，过拟合更容易发生。此外，泛化误差不会随训练数据集里样本数量增加而增大。因此，在计算资源允许的范围之内，我们通常希望训练数据集大一些，特别是在模型复杂度较高时，如层数较多的深度学习模型。
图3-4 模型复杂度对欠拟合和过拟合的影响
为了理解模型复杂度和训练数据集大小对欠拟合和过拟合的影响，下面我们以多项式函数拟合为例来实验。首先导入实验需要的包或模块。
In [1]: %matplotlib inline
import d2lzh as d2l
from mxnet import autograd, gluon, nd
from mxnet.gluon import data as gdata, loss as gloss, nn我们将生成一个人工数据集。在训练数据集和测试数据集中，给定样本特征x，我们使用如下的三阶多项式函数来生成该样本的标签：
其中噪声项ϵ服从均值为 0 、标准差为 0.1 的正态分布。训练数据集和测试数据集的样本数都设为 100。
In [2]: n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = nd.random.normal(shape=(n_train + n_test, 1))
poly_features = nd.concat(features, nd.power(features, 2),
nd.power(features, 3))
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]
+ true_w[2] * poly_features[:, 2] + true_b)
labels += nd.random.normal(scale=0.1, shape=labels.shape)看一看生成的数据集的前两个样本。
In [3]: features[:2], poly_features[:2], labels[:2]
Out[3]: (
[[2.2122064]
[0.7740038]]
<NDArray 2x1 @cpu(0)>,
[[ 2.2122064 4.893857 10.826221 ]
[ 0.7740038 0.5990819 0.46369165]]
<NDArray 2x3 @cpu(0)>,
[51.674885 6.3585763]
<NDArray 2 @cpu(0)>)我们先定义作图函数semilogy，其中 y轴使用了对数尺度。
In [4]: # 本函数已保存在d2lzh包中方便以后使用
def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,
legend=None, f igsize=(3.5, 2.5)):
d2l.set_f igsize(f igsize)
d2l.plt.xlabel(x_label)
d2l.plt.ylabel(y_label)
d2l.plt.semilogy(x_vals, y_vals)
if x2_vals and y2_vals:
d2l.plt.semilogy(x2_vals, y2_vals, linestyle=':')
d2l.plt.legend(legend)和线性回归一样，多项式函数拟合也使用平方损失函数。因为我们将尝试使用不同复杂度的模型来拟合生成的数据集，所以我们把模型定义部分放在fit_and_plot函数中。多项式函数拟合的训练和测试步骤与3.6节介绍的 softmax 回归中的相关步骤类似。
In [5]: num_epochs, loss = 100, gloss.L2Loss()
def f it_and_plot(train_features, test_features, train_labels, test_labels):
net = nn.Sequential()
net.add(nn.Dense(1))
net.initialize()
batch_size = min(10, train_labels.shape[0])
train_iter = gdata.DataLoader(gdata.ArrayDataset(
train_features, train_labels), batch_size, shuff le=True)
trainer = gluon.Trainer(net.collect_params(), 'sgd',
{'learning_rate': 0.01})
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
with autograd.record():
l = loss(net(X), y)
l.backward()
trainer.step(batch_size)
train_ls.append(loss(net(train_features),
train_labels).mean().asscalar())
test_ls.append(loss(net(test_features),
test_labels).mean().asscalar())
print('f inal epoch: train loss', train_ls[-1], 'test loss', test_ls[-1])
semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
print('weight:', net[0].weight.data().asnumpy(),
'\nbias:', net[0].bias.data().asnumpy())我们先使用与数据生成函数同阶的三阶多项式函数拟合。实验表明，这个模型的训练误差和在测试数据集的误差都较低。训练出的模型参数也接近真实值：
。
In [6]: f it_and_plot(poly_features[:n_train, :], poly_features[n_train:, :],
labels[:n_train], labels[n_train:])
f inal epoch: train loss 0.007049637 test loss 0.0119097745
weight: [[ 1.3258897 -3.363281 5.561593 ]]
bias: [4.9517436]我们再试试线性函数拟合。很明显，该模型的训练误差在迭代早期下降后便很难继续降低。在完成最后一次迭代周期后，训练误差依旧很高。线性模型在非线性模型（如三阶多项式函数）生成的数据集上容易欠拟合。
In [7]: f it_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train],
labels[n_train:])
f inal epoch: train loss 43.997887 test loss 160.65588
weight: [[15.577538]]
bias: [2.2902575]事实上，即便使用与数据生成模型同阶的三阶多项式函数模型，如果训练样本不足，该模型依然容易过拟合。让我们只使用两个样本来训练模型。显然，训练样本过少了，甚至少于模型参数的数量。这使模型显得过于复杂，以至于容易被训练数据中的噪声影响。在迭代过程中，尽管训练误差较低，但是测试数据集上的误差却很高。这是典型的过拟合现象。
In [8]: f it_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2],
labels[n_train:])
f inal epoch: train loss 0.4027369 test loss 103.314186
weight: [[1.3872364 1.9376589 3.5085924]]
bias: [1.2312856]我们将在3.12节和3.13节继续讨论过拟合问题以及应对过拟合的方法。
小结
- 由于无法从训练误差估计泛化误差，一味地降低训练误差并不意味着泛化误差一定会降低。机器学习模型应关注降低泛化误差。
- 可以使用验证数据集来进行模型选择。
- 欠拟合指模型无法得到较低的训练误差，过拟合指模型的训练误差远小于它在测试数据集上的误差。
- 应选择复杂度合适的模型并避免使用过少的训练样本。
练习
（1）如果用一个三阶多项式模型来拟合一个线性模型生成的数据，可能会有什么问题？为什么？
（2）在本节提到的三阶多项式拟合问题里，有没有可能把 100 个样本的训练误差的期望降到 0，为什么？（提示：考虑噪声的存在。）
扫码直达讨论区
3.11节中我们观察了过拟合现象，即模型的训练误差远小于它在测试集上的误差。虽然增大训练数据集可能会减轻过拟合，但是获取额外的训练数据往往代价高昂。本节介绍应对过拟合问题的常用方法——权重衰减（weight decay）。
权重衰减等价于
范数正则化（regularization）。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。我们先描述范数正则化，再解释它为何又称权重衰减。
范数正则化在模型原损失函数基础上添加 范数惩罚项，从而得到训练所需要最小化的函数。范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以3.1节中的线性回归损失函数
为例，其中
, 是权重参数，b 是偏差参数，样本 i 的输入为
，标签为
，样本数为n。将权重参数用向量
表示，带有 范数惩罚项的新损失函数为
其中超参数
。当权重参数均为 0 时，惩罚项最小。当
较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近 0。当设为 0 时，惩罚项完全不起作用。上式中范数平方
展开后得到
。有了范数惩罚项后，在小批量随机梯度下降中，我们将3.1节中权重
和
的迭代方式更改为
可见，范数正则化令权重和先自乘小于 1 的数，再减去不含惩罚项的梯度。因此， 范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制，这可能对过拟合有效。实际场景中，我们有时也在惩罚项中添加偏差元素的平方和。
下面，我们以高维线性回归为例来引入一个过拟合问题，并使用权重衰减来应对过拟合。设数据样本特征的维度为p。对于训练数据集和测试数据集中特征为
的任一样本，我们使用如下的线性函数来生成该样本的标签：
其中噪声项ϵ服从均值为 0、标准差为 0.01 的正态分布。为了较容易地观察过拟合，我们考虑高维线性回归问题，如设维度p=200；同时，我们特意把训练数据集的样本数设低，如 20。
In [1]: %matplotlib inline
import d2lzh as d2l
from mxnet import autograd, gluon, init, nd
from mxnet.gluon import data as gdata, loss as gloss, nn
n_train, n_test, num_inputs = 20, 100, 200
true_w, true_b = nd.ones((num_inputs, 1)) * 0.01, 0.05
features = nd.random.normal(shape=(n_train + n_test, num_inputs))
labels = nd.dot(features, true_w) + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)
train_features, test_features = features[:n_train, :], features[n_train:, :]
train_labels, test_labels = labels[:n_train], labels[n_train:]下面先介绍从零开始实现权重衰减的方法。我们通过在目标函数后添加L2范数惩罚项来实现权重衰减。
首先，定义随机初始化模型参数的函数。该函数为每个参数都附上梯度。
In [2]: def init_params():
w = nd.random.normal(scale=1, shape=(num_inputs, 1))
b = nd.zeros(shape=(1,))
w.attach_grad()
b.attach_grad()
return [w, b]下面定义L2范数惩罚项。这里只惩罚模型的权重参数。
In [3]: def l2_penalty(w):
return (w**2).sum() / 2下面定义如何在训练数据集和测试数据集上分别训练和测试模型。与前面几节中不同的是，这里在计算最终的损失函数时添加了L2范数惩罚项。
In [4]: batch_size, num_epochs, lr = 1, 100, 0.003
net, loss = d2l.linreg, d2l.squared_loss
train_iter = gdata.DataLoader(gdata.ArrayDataset(
train_features, train_labels), batch_size, shuff le=True)
def f it_and_plot(lambd):
w, b = init_params()
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
with autograd.record():
# 添加了L2范数惩罚项
l = loss(net(X, w, b), y) + lambd * l2_penalty(w)
l.backward()
d2l.sgd([w, b], lr, batch_size)
train_ls.append(loss(net(train_features, w, b),
train_labels).mean().asscalar())
test_ls.append(loss(net(test_features, w, b),
test_labels).mean().asscalar())
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
print('L2 norm of w:', w.norm().asscalar())接下来，让我们训练并测试高维线性回归模型。当lambd设为 0 时，我们没有使用权重衰减。结果训练误差远小于测试集上的误差。这是典型的过拟合现象。
In [5]: f it_and_plot(lambd=0)L2 norm of w: 11.611939下面我们使用权重衰减。可以看出，训练误差虽然有所提高，但测试集上的误差有所下降。过拟合现象得到一定程度的缓解。另外，权重参数的范数比不使用权重衰减时的更小，此时的权重参数更接近 0。
In [6]: f it_and_plot(lambd=3)L2 norm of w: 0.041881386这里我们直接在构造Trainer实例时通过wd参数来指定权重衰减超参数。默认下，Gluon 会对权重和偏差同时衰减。我们可以分别对权重和偏差构造Trainer实例，从而只对权重衰减。
In [7]: def f it_and_plot_gluon(wd):
net = nn.Sequential()
net.add(nn.Dense(1))
net.initialize(init.Normal(sigma=1))
# 对权重参数衰减。权重名称一般是以weight结尾
trainer_w = gluon.Trainer(net.collect_params('.*weight'), 'sgd',
{'learning_rate': lr, 'wd': wd})
# 不对偏差参数衰减。偏差名称一般是以bias结尾
trainer_b = gluon.Trainer(net.collect_params('.*bias'), 'sgd',
{'learning_rate': lr})
train_ls, test_ls = [], []
for _ in range(num_epochs):
for X, y in train_iter:
with autograd.record():
l = loss(net(X), y)
l.backward()
# 对两个Trainer实例分别调用step函数, 从而分别更新权重和偏差
trainer_w.step(batch_size)
trainer_b.step(batch_size)
train_ls.append(loss(net(train_features),
train_labels).mean().asscalar())
test_ls.append(loss(net(test_features),
test_labels).mean().asscalar())
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
print('L2 norm of w:', net[0].weight.data().norm().asscalar()) 与从零开始实现权重衰减的实验现象类似，使用权重衰减可以在一定程度上缓解过拟合问题。
In [8]: f it_and_plot_gluon(0)L2 norm of w: 13.311797
In [9]: f it_and_plot_gluon(3)L2 norm of w: 0.032021914小结
- 正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。
- 权重衰减等价于
- 权重衰减可以通过 Gluon 的
wd超参数来指定。- 可以定义多个
Trainer实例对不同的模型参数使用不同的迭代方法。练习
（1）回顾一下训练误差和泛化误差的关系。除了权重衰减、增大训练量以及使用复杂度合适的模型，你还能想到哪些办法来应对过拟合？
（2）如果你了解贝叶斯统计，你觉得权重衰减对应贝叶斯统计里的哪个重要概念？
（3）调节实验中的权重衰减超参数，观察并分析实验结果。
扫码直达讨论区
除了3.12节介绍的权重衰减以外，深度学习模型常常使用丢弃法（dropout）[49] 来应对过拟合问题。丢弃法有一些不同的变体。本节中提到的丢弃法特指倒置丢弃法（inverted dropout）。
回忆一下，3.8节的图3-3描述了一个含单隐藏层的多层感知机。其中输入个数为 4，隐藏单元个数为 5，且隐藏单元
(
)的计算表达式为
这里
是激活函数，
是输入，隐藏单元i的权重参数为
，偏差参数为
。当对该隐藏层使用丢弃法时，该层的隐藏单元将有一定概率被丢弃掉。设丢弃概率为p，那么有p的概率 会被清零，有
的概率 会除以做拉伸。丢弃概率是丢弃法的超参数。具体来说，设随机变量
为0和1的概率分别为p和。使用丢弃法时我们计算新的隐藏单元
由于，因此
即丢弃法不改变其输入的期望值。让我们对图3-3中的隐藏层使用丢弃法，一种可能的结果如图3-5所示，其中
和
被清零。这时输出值的计算不再依赖和，在反向传播时，与这两个隐藏单元相关的权重的梯度均为 0。由于在训练中隐藏层神经元的丢弃是随机的，即
都有可能被清零，输出层的计算无法过度依赖中的任一个，从而在训练模型时起到正则化的作用，并可以用来应对过拟合。在测试模型时，我们为了得到更加确定性的结果，一般不使用丢弃法。
图3-5 隐藏层使用了丢弃法的多层感知机
根据丢弃法的定义，我们可以很容易地实现它。下面的dropout函数将以drop_prob的概率丢弃NDArray 输入X中的元素。
In [1]: import d2lzh as d2l
from mxnet import autograd, gluon, init, nd
from mxnet.gluon import loss as gloss, nn
def dropout(X, drop_prob):
assert 0 <= drop_prob <= 1
keep_prob = 1 - drop_prob
# 这种情况下把全部元素都丢弃
if keep_prob == 0:
return X.zeros_like()
mask = nd.random.uniform(0, 1, X.shape) < keep_prob
return mask * X / keep_prob 我们运行几个例子来测试一下dropout函数，其中丢弃概率分别为 0、0.5 和 1。
In [2]: X = nd.arange(16).reshape((2, 8))
dropout(X, 0)
Out[2]:
[[ 0. 1. 2. 3. 4. 5. 6. 7.]
[ 8. 9. 10. 11. 12. 13. 14. 15.]]
<NDArray 2x8 @cpu(0)>
In [3]: dropout(X, 0.5)
Out[3]:
[[ 0. 2. 4. 6. 0. 0. 0. 14.]
[ 0. 18. 0. 0. 24. 26. 28. 0.]]
<NDArray 2x8 @cpu(0)>
In [4]: dropout(X, 1)
Out[4]:
[[0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0.]]
<NDArray 2x8 @cpu(0)>实验中，我们依然使用3.5节中介绍的 Fashion-MNIST 数据集。我们将定义一个包含两个隐藏层的多层感知机，其中两个隐藏层的输出个数都是 256。
In [5]: num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
W1 = nd.random.normal(scale=0.01, shape=(num_inputs, num_hiddens1))
b1 = nd.zeros(num_hiddens1)
W2 = nd.random.normal(scale=0.01, shape=(num_hiddens1, num_hiddens2))
b2 = nd.zeros(num_hiddens2)
W3 = nd.random.normal(scale=0.01, shape=(num_hiddens2, num_outputs))
b3 = nd.zeros(num_outputs)
params = [W1, b1, W2, b2, W3, b3]
for param in params:
param.attach_grad()下面定义的模型将全连接层和激活函数ReLU串起来，并对每个激活函数的输出使用丢弃法。我们可以分别设置各个层的丢弃概率。通常的建议是把靠近输入层的丢弃概率设得小一点。在这个实验中，我们把第一个隐藏层的丢弃概率设为0.2，把第二个隐藏层的丢弃概率设为0.5。我们可以通过2.3节中介绍的is_training函数来判断运行模式为训练还是测试，并只需在训练模式下使用丢弃法。
In [6]: drop_prob1, drop_prob2 = 0.2, 0.5
def net(X):
X = X.reshape((-1, num_inputs))
H1 = (nd.dot(X, W1) + b1).relu()
if autograd.is_training(): # 只在训练模型时使用丢弃法
H1 = dropout(H1, drop_prob1) # 在第一层全连接后添加丢弃层
H2 = (nd.dot(H1, W2) + b2).relu()
if autograd.is_training():
H2 = dropout(H2, drop_prob2) # 在第二层全连接后添加丢弃层
return nd.dot(H2, W3) + b3这部分与之前多层感知机的训练和测试类似。
In [7]: num_epochs, lr, batch_size = 5, 0.5, 256
loss = gloss.SoftmaxCrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params, lr)
epoch 1, loss 1.2260, train acc 0.526, test acc 0.759
epoch 2, loss 0.6336, train acc 0.765, test acc 0.795
epoch 3, loss 0.5147, train acc 0.812, test acc 0.845
epoch 4, loss 0.4648, train acc 0.830, test acc 0.861
epoch 5, loss 0.4362, train acc 0.840, test acc 0.852在 Gluon 中，我们只需要在全连接层后添加Dropout层并指定丢弃概率。在训练模型时，Dropout层将以指定的丢弃概率随机丢弃上一层的输出元素；在测试模型时，Dropout层并不发挥作用。
In [8]: net = nn.Sequential()
net.add(nn.Dense(256, activation="relu"),
nn.Dropout(drop_prob1), # 在第一个全连接层后添加丢弃层
nn.Dense(256, activation="relu"),
nn.Dropout(drop_prob2), # 在第二个全连接层后添加丢弃层
nn.Dense(10))
net.initialize(init.Normal(sigma=0.01))下面训练并测试模型。
In [9]: trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr})
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None,
None, trainer)
epoch 1, loss 1.1863, train acc 0.542, test acc 0.765
epoch 2, loss 0.5867, train acc 0.782, test acc 0.839
epoch 3, loss 0.4947, train acc 0.821, test acc 0.857
epoch 4, loss 0.4476, train acc 0.839, test acc 0.865
epoch 5, loss 0.4224, train acc 0.845, test acc 0.864小结
- 我们可以通过使用丢弃法应对过拟合。
- 丢弃法只在训练模型时使用。
练习
（1）如果把本节中的两个丢弃概率超参数对调，会有什么结果？
（2）增大迭代周期数，比较使用丢弃法与不使用丢弃法的结果。
（3）如果将模型改得更加复杂，如增加隐藏层单元，使用丢弃法应对过拟合的效果是否更加明显？
（4）以本节中的模型为例，比较使用丢弃法与权重衰减的效果。如果同时使用丢弃法和权重衰减，效果会如何？
扫码直达讨论区
前面几节里我们使用了小批量随机梯度下降的优化算法来训练模型。在实现中，我们只提供了模型的正向传播的计算，即对输入计算模型输出，然后通过autograd模块来调用系统自动生成的backward函数计算梯度。基于反向传播算法的自动求梯度极大简化了深度学习模型训练算法的实现。本节我们将使用数学来描述正向传播和反向传播。具体来说，我们将以带范数正则化的含单隐藏层的多层感知机为样例模型解释正向传播和反向传播。
正向传播（forward-propagation）是指对神经网络沿着从输入层到输出层的顺序，依次计算并存储模型的中间变量（包括输出）。为简单起见，假设输入是一个特征为
的样本，且不考虑偏差项，那么中间变量
其中
是隐藏层的权重参数。把中间变量
输入按元素运算的激活函数后，将得到向量长度为h的隐藏层变量
隐藏层变量h也是一个中间变量。假设输出层参数只有权重
，可以得到向量长度为q的输出层变量
假设损失函数为
，且样本标签为 y，可以计算出单个数据样本的损失项
根据范数正则化的定义，给定超参数λ，正则化项即
其中矩阵的Frobenius范数等价于将矩阵变平为向量后计算范数。最终，模型在给定的数据样本上带正则化的损失为
我们将J称为有关给定数据样本的目标函数，并在以下的讨论中简称目标函数。
我们通常绘制计算图（computational graph）来可视化运算符和变量在计算中的依赖关系。图3-6绘制了本节中样例模型正向传播的计算图，其中左下角是输入，右上角是输出。可以看到，图中箭头方向大多是向右和向上，其中方框代表变量，圆圈代表运算符，箭头表示从输入到输出之间的依赖关系。
图3-6 正向传播的计算图
反向传播（back-propagation）指的是计算神经网络参数梯度的方法。总的来说，反向传播依据微积分中的链式法则，沿着从输出层到输入层的顺序，依次计算并存储目标函数有关神经网络各层的中间变量以及参数的梯度。对输入或输出X, Y, Z为任意形状张量的函数
和
，通过链式法则，我们有
其中prod运算符将根据两个输入的形状，在必要的操作（如转置和互换输入位置）后对两个输入做乘法。
回顾一下本节中样例模型，它的参数是
和
，因此反向传播的目标是计算
和
。我们将应用链式法则依次计算各中间变量和参数的梯度，其计算次序与前向传播中相应中间变量的计算次序恰恰相反。首先，分别计算目标函数
有关损失项L和正则项s的梯度
其次，依据链式法则计算目标函数有关输出层变量的梯度
：
接下来，计算正则项有关两个参数的梯度：
现在，我们可以计算最靠近输出层的模型参数的梯度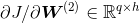
。依据链式法则，得到
沿着输出层向隐藏层继续反向传播，隐藏层变量的梯度
可以这样计算：
由于激活函数是按元素运算的，中间变量
的梯度
的计算需要使用按元素乘法符
：
最终，我们可以得到最靠近输入层的模型参数的梯度
。依据链式法则，得到
在训练深度学习模型时，正向传播和反向传播之间相互依赖。下面我们仍然以本节中的样例模型分别阐述它们之间的依赖关系。
一方面，正向传播的计算可能依赖于模型参数的当前值，而这些模型参数是在反向传播的梯度计算后通过优化算法迭代的。例如，计算正则化项
依赖模型参数和 的当前值，而这些当前值是优化算法最近一次根据反向传播算出梯度后迭代得到的。
另一方面，反向传播的梯度计算可能依赖于各变量的当前值，而这些变量的当前值是通过正向传播计算得到的。举例来说，参数梯度
的计算需要依赖隐藏层变量的当前值h。这个当前值是通过从输入层到输出层的正向传播计算并存储得到的。
因此，在模型参数初始化完成后，我们交替地进行正向传播和反向传播，并根据反向传播计算的梯度迭代模型参数。既然我们在反向传播中使用了正向传播中计算得到的中间变量来避免重复计算，那么这个复用也导致正向传播结束后不能立即释放中间变量内存。这也是训练要比预测占用更多内存的一个重要原因。另外需要指出的是，这些中间变量的个数大体上与网络层数线性相关，每个变量的大小与批量大小和输入个数也是线性相关的，它们是导致较深的神经网络使用较大批量训练时更容易超内存的主要原因。
小结
- 正向传播沿着从输入层到输出层的顺序，依次计算并存储神经网络的中间变量。
- 反向传播沿着从输出层到输入层的顺序，依次计算并存储神经网络的中间变量和参数的梯度。
- 在训练深度学习模型时，正向传播和反向传播相互依赖。
练习
在本节样例模型的隐藏层和输出层中添加偏差参数，修改计算图以及正向传播和反向传播的数学表达式。
扫码直达讨论区
理解了正向传播与反向传播以后，我们来讨论一下深度学习模型的数值稳定性问题以及模型参数的初始化方法。深度模型有关数值稳定性的典型问题是衰减（vanishing）和爆炸（explosion）。
当神经网络的层数较多时，模型的数值稳定性容易变差。假设一个层数为L 的多层感知机的第l 层
的权重参数为
，输出层
的权重参数为
。为了便于讨论，不考虑偏差参数，且设所有隐藏层的激活函数为恒等映射（identity mapping）
。给定输入
，多层感知机的第l层的输出
。此时，如果层数l较大，的计算可能会出现衰减或爆炸。举个例子，假设输入和所有层的权重参数都是标量，如权重参数为0.2和5，多层感知机的第 30 层输出为输入分别与0.230≈1×10-21（衰减）和530≈9×1020（爆炸）的乘积。类似地，当层数较多时，梯度的计算也更容易出现衰减或爆炸。
随着内容的不断深入，我们会在后面的章节进一步介绍深度学习的数值稳定性问题以及解决方法。
在神经网络中，通常需要随机初始化模型参数。下面我们来解释这样做的原因。
回顾3.8节图3-3 描述的多层感知机。为了方便解释，假设输出层只保留一个输出单元o1（删去o2和o3以及指向它们的箭头），且隐藏层使用相同的激活函数。如果将每个隐藏单元的参数都初始化为相等的值，那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值，并传递至输出层。在反向传播中，每个隐藏单元的参数梯度值相等。因此，这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下，无论隐藏单元有多少，隐藏层本质上只有 1 个隐藏单元在发挥作用。因此，正如在前面的实验中所做的那样，我们通常对神经网络的模型参数，特别是权重参数，进行随机初始化。
随机初始化模型参数的方法有很多。在3.3节中，我们使用net.initialize(init.Normal(sigma=0.01))使模型net的权重参数采用正态分布的随机初始化方式。如果不指定初始化方法，如net.initialize()，MXNet 将使用默认的随机初始化方法：权重参数每个元素随机采样于-0.07 到0.07之间的均匀分布，偏差参数全部清零。
还有一种比较常用的随机初始化方法叫作Xavier随机初始化[16]。假设某全连接层的输入个数为a，输出个数为b，Xavier 随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布
它的设计主要考虑到，模型参数初始化后，每层输出的方差不该受该层输入个数影响，且每层梯度的方差也不该受该层输出个数影响。
小结
- 深度模型有关数值稳定性的典型问题是衰减和爆炸。当神经网络的层数较多时，模型的数值稳定性容易变差。
- 我们通常需要随机初始化神经网络的模型参数，如权重参数。
练习
（1）有人说随机初始化模型参数是为了“打破对称性”。这里的“对称”应如何理解？
（2）是否可以将线性回归或 softmax 回归中所有的权重参数都初始化为相同值？
扫码直达讨论区
作为深度学习基础篇章的总结，我们将对本章内容学以致用。下面，让我们动手实战一个 Kaggle 比赛——房价预测。本节将提供未经调优的数据的预处理、模型的设计和超参数的选择。我们希望读者通过动手操作、仔细观察实验现象、认真分析实验结果并不断调整方法，得到令自己满意的结果。
Kaggle是一个著名的供机器学习爱好者交流的平台。图3-7展示了 Kaggle 网站的首页。为了便于提交结果，需要注册 Kaggle 账号。
图3-7 Kaggle网站的首页
我们可以在房价预测比赛的网页上了解比赛信息和参赛者成绩，也可以下载数据集并提交自己的预测结果。该比赛的网页地址是https://www.kaggle.com/c/house-prices-advanced-regression-techniques。
图3-8展示了房价预测比赛的网页信息。
图3-8 房价预测比赛的网页信息。比赛数据集可通过点击“Data”标签获取
比赛数据分为训练数据集和测试数据集。两个数据集都包括每栋房子的特征，如街道类型、建造年份、房顶类型、地下室状况等特征值。这些特征值有连续的数字、离散的标签甚至是缺失值“na”。只有训练数据集包括了每栋房子的价格，也就是标签。我们可以访问比赛网页，点击图3-8中的“Data”标签，并下载这些数据集。
我们将通过pandas库读取并处理数据。在导入本节需要的包前请确保已安装pandas库，否则请参考下面的代码注释。
In [1]: # 如果没有安装pandas, 则反注释下面一行
# !pip install pandas
%matplotlib inline
import d2lzh as d2l
from mxnet import autograd, gluon, init, nd
from mxnet.gluon import data as gdata, loss as gloss, nn
import numpy as np
import pandas as pd 解压后的数据位于../data目录，它包括两个 csv 文件。下面使用pandas读取这两个文件。
In [2]: train_data = pd.read_csv('../data/kaggle_house_pred_train.csv')
test_data = pd.read_csv('../data/kaggle_house_pred_test.csv')训练数据集包括 1 460 个样本、80 个特征和 1 个标签。
In [3]: train_data.shape
Out[3]: (1460, 81)测试数据集包括 1 459 个样本和 80 个特征。我们需要将测试数据集中每个样本的标签预测出来。
In [4]: test_data.shape
Out[4]: (1459, 80)让我们来查看前 4 个样本的前 4 个特征、后 2 个特征和标签（SalePrice）：
In [5]: train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]]
Out[5]: Id MSSubClass MSZoning LotFrontage SaleType SaleCondition SalePrice
0 1 60 RL 65.0 WD Normal 208500
1 2 20 RL 80.0 WD Normal 181500
2 3 60 RL 68.0 WD Normal 223500
3 4 70 RL 60.0 WD Abnorml 140000可以看到第一个特征是 Id，它能帮助模型记住每个训练样本，但难以推广到测试样本，所以我们不使用它来训练。我们将所有的训练数据和测试数据的79个特征按样本连结。
In [6]: all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))我们对连续数值的特征做标准化（standardization）：设该特征在整个数据集上的均值为µ，标准差为σ。那么，我们可以将该特征的每个值先减去µ再除以σ得到标准化后的每个特征值。对于缺失的特征值，我们将其替换成该特征的均值。
In [7]: numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply(
lambda x: (x - x.mean()) / (x.std()))
# 标准化后, 每个特征的均值变为0, 所以可以直接用0来替换缺失值
all_features[numeric_features] = all_features[numeric_features].f illna(0)接下来将离散数值转成指示特征。举个例子，假设特征 MSZoning 里面有两个不同的离散值 RL 和 RM，那么这一步转换将去掉 MSZoning 特征，并新加两个特征 MSZoning_RL 和 MSZoning_RM，其值为 0 或 1。如果一个样本原来在 MSZoning 里的值为 RL，那么有 MSZoning_RL = 1 且 MSZoning_RM = 0。
In [8]: # dummy_na=True将缺失值也当作合法的特征值并为其创建指示特征
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape
Out[8]: (2919, 331)可以看到这一步转换将特征数从 79 增加到了 331。
最后，通过values属性得到NumPy 格式的数据，并转成NDArray方便后面的训练。
In [9]: n_train = train_data.shape[0]
train_features = nd.array(all_features[:n_train].values)
test_features = nd.array(all_features[n_train:].values)
train_labels = nd.array(train_data.SalePrice.values).reshape((-1, 1))我们使用一个基本的线性回归模型和平方损失函数来训练模型。
In [10]: loss = gloss.L2Loss()
def get_net():
net = nn.Sequential()
net.add(nn.Dense(1))
net.initialize()
return net下面定义比赛用来评价模型的对数均方根误差。给定预测值
和对应的真实标签
，它的定义为
对数均方根误差的实现如下：
In [11]: def log_rmse(net, features, labels):
# 将小于1的值设成1, 使得取对数时数值更稳定
clipped_preds = nd.clip(net(features), 1, f loat('inf'))
rmse = nd.sqrt(2 * loss(clipped_preds.log(), labels.log()).mean())
return rmse.asscalar()下面的训练函数与本章中前几节的不同在于使用了 Adam 优化算法。相对之前使用的小批量随机梯度下降，它对学习率相对不那么敏感。我们将在7.8节详细介绍它。
In [12]: def train(net, train_features, train_labels, test_features, test_labels,
num_epochs, learning_rate, weight_decay, batch_size):
train_ls, test_ls = [], []
train_iter = gdata.DataLoader(gdata.ArrayDataset(
train_features, train_labels), batch_size, shuff le=True)
# 这里使用了Adam优化算法
trainer = gluon.Trainer(net.collect_params(), 'adam', {
'learning_rate': learning_rate, 'wd': weight_decay})
for epoch in range(num_epochs):
for X, y in train_iter:
with autograd.record():
l = loss(net(X), y)
l.backward()
trainer.step(batch_size)
train_ls.append(log_rmse(net, train_features, train_labels))
if test_labels is not None:
test_ls.append(log_rmse(net, test_features, test_labels))
return train_ls, test_ls我们在3.11节中介绍了k折交叉验证。它将被用来选择模型设计并调节超参数。下面实现了一个函数，它返回第i折交叉验证时所需要的训练和验证数据。
In [13]: def get_k_fold_data(k, i, X, y):
assert k > 1
fold_size = X.shape[0] // k
X_train, y_train = None, None
for j in range(k):
idx = slice(j * fold_size, (j + 1) * fold_size)
X_part, y_part = X[idx, :], y[idx]
if j == i:
X_valid, y_valid = X_part, y_part
elif X_train is None:
X_train, y_train = X_part, y_part
else:
X_train = nd.concat(X_train, X_part, dim=0)
y_train = nd.concat(y_train, y_part, dim=0)
return X_train, y_train, X_valid, y_valid 在k折交叉验证中我们训练k 次并返回训练和验证的平均误差。
In [14]: def k_fold(k, X_train, y_train, num_epochs,
learning_rate, weight_decay, batch_size):
train_l_sum, valid_l_sum = 0, 0
for i in range(k):
data = get_k_fold_data(k, i, X_train, y_train)
net = get_net()
train_ls, valid_ls = train(net, *data, num_epochs, learning_rate,
weight_decay, batch_size)
train_l_sum += train_ls[-1]
valid_l_sum += valid_ls[-1]
if i == 0:
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse',
range(1, num_epochs + 1), valid_ls,
['train', 'valid'])
print('fold %d, train rmse %f, valid rmse %f'
% (i, train_ls[-1], valid_ls[-1]))
return train_l_sum / k, valid_l_sum / k我们使用一组未经调优的超参数并计算交叉验证误差。可以改动这些超参数来尽可能减小平均测试误差。
In [15]: k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr,
weight_decay, batch_size)
print('%d-fold validation: avg train rmse %f, avg valid rmse %f'
% (k, train_l, valid_l))fold 0, train rmse 0.169686, valid rmse 0.157010
fold 1, train rmse 0.162097, valid rmse 0.187972
fold 2, train rmse 0.163778, valid rmse 0.168125
fold 3, train rmse 0.167723, valid rmse 0.154744
fold 4, train rmse 0.162573, valid rmse 0.182765
5-fold validation: avg train rmse 0.165172, avg valid rmse 0.170123有时候你会发现一组参数的训练误差可以达到很低，但是在k折交叉验证上的误差可能反而较高。这种现象很可能是由过拟合造成的。因此，当训练误差降低时，我们要观察k折交叉验证上的误差是否也相应降低。
下面定义预测函数。在预测之前，我们会使用完整的训练数据集来重新训练模型，并将预测结果存成提交所需要的格式。
In [16]: def train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size):
net = get_net()
train_ls, _ = train(net, train_features, train_labels, None, None,
num_epochs, lr, weight_decay, batch_size)
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse')
print('train rmse %f' % train_ls[-1])
preds = net(test_features).asnumpy()
test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
submission.to_csv('submission.csv', index=False)设计好模型并调好超参数之后，下一步就是对测试数据集上的房屋样本做价格预测。如果我们得到与交叉验证时差不多的训练误差，那么这个结果很可能是理想的，可以在 Kaggle 上提交结果。
In [17]: train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size)train rmse 0.162369上述代码执行完之后会生成一个submission.csv文件。这个文件是符合 Kaggle 比赛要求的提交格式的。这时，我们可以在Kaggle上提交我们预测得出的结果，并且查看与测试数据集上真实房价（标签）的误差。具体来说有以下几个步骤：登录Kaggle网站，访问房价预测比赛网页，并点击右侧“Submit Predictions”或“Late Submission”按钮；然后，点击页面下方“Upload Submission File”图标所在的虚线框选择需要提交的预测结果文件；最后，点击页面最下方的“Make Submission”按钮就可以查看结果了，如图 3-9 所示。
图3-9 Kaggle预测房价比赛的预测结果提交页面
小结
- 通常需要对真实数据做预处理。
- 可以使用k折交叉验证来选择模型并调节超参数。
练习
（1）在 Kaggle 提交本节的预测结果。观察一下，这个结果在 Kaggle 上能拿到什么样的分数？
（2）对照k折交叉验证结果，不断修改模型（例如添加隐藏层）和调参，能提高 Kaggle 上的分数吗？
（3）如果不使用本节中对连续数值特征的标准化处理，结果会有什么变化?
（4）扫码直达讨论区，在社区交流方法和结果。你能发掘出其他更好的技巧吗？
